Mетод гармонической линеаризации

Mетод гармонической линеаризации представляет собой приближенный метод, основанный на принципе гармонического баланса, т.е. эквивалентной линеаризации. При этом для приближенного исследования используется линейная теория систем автоматического управления, что основано на концепции фильтра линейной части САУ и предположении о гармоническом характере свободного движения в нелинейной системе.

Структурная схема САУ, содержащей нелинейный элемент (НЭ) , включенный последовательно в цепь прохождения основного сигнала, показана на рис.2. Структурную схему можно представить в виде линейной части с передаточной функцией 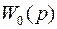, включающей передаточные функции исполнительного элемента ИЭ , объекта регулирования ОР , элемента обратной связи ОС  и нелинейного элемента с передаточной функцией W _нэ(p) с нелинейной характеристикой j(σ).

Рис.2. Структурная схема САУ с нелинейным элементом

Рассмотрим прохождение гармонического сигнала через разомкнутую нелинейную систему, при условии, что сигнал на входе нелинейного элемента является синусоидальным:

.

Сигнал на выходе нелинейного элемента:

.

Функция является периодической и может быть разложена в ряд Фурье:

.

Для симметричных однозначных характеристик отсутствуют четные гармоники и коэффициенты B_k.

Т.о. на линейную часть САУ действует весь спектр частот. В силу принципа суперпозиции (наложения) каждая гармоника действует на линейную часть независимо от других гармоник. Следовательно, на выходе САУ создаются негармонические колебания. Их спектр будет содержать все те же частоты, что и спектр гармоник на входе нелинейного элемента, но амплитуда каждой гармоники будет зависеть от свойств линейной части и изменяться в  раз.

Амплитудно-частотная характеристика линейной части (рис.3) позволяет установить, во сколько раз изменяются амплитуды всех гармоник, порожденных нелинейным элементом, при прохождении их через линейную часть САУ. Для этого надо при заданном значении частоты ω₁ основной гармоники рассмотреть ординаты амплитудно-частотной характеристики при ω₁, 3ω₁, 5ω₁ и т.д. Если ордината  при частоте ω₁ несоизмеримо больше амплитуд более высоких гармоник, то линейная часть системы является фильтром и не пропускает высшие гармоники, порождаемые нелинейным элементом САУ.

Рис. 3. Амплитудно-частотная характеристика линейной части САУ

 

Если в замкнутой САУ имеются автоколебания, следовательно, при входном сигнале X_вх=0 в контуре системы имеется сигнал, обеспечивающий автоколебательный режим.

Приближенное определение автоколебаний в нелинейной системе базируется на допущении, что на вход нелинейного элемента поступает гармонический сигнал, а линейная часть САУ гасит все высшие гармоники, порождаемые нелинейностью. Это позволяет производить гармоническую линеаризацию нелинейной характеристики и исследовать по гармонически линеаризованному уравнению методами линейной теории.

Гармоническая линеаризация нелинейной характеристики заключается в том, что записывается ряд Фурье для выходной переменной нелинейного элемента при гармоническом входном сигнале. Далее используется только первая гармоника, в результате получается аналитическая линейная зависимость между входным гармоническим сигналом и выходным гармоническим сигналом нелинейного элемента.

    Для однозначных симметричных нелинейных характеристик (рис.1, б, в, г) выходной гармонический сигнал нелинейного элемента:

;

Или                          .

Здесь     .

Для замкнутой нелинейной системы сигнал на входе нелинейного элемента равен выходной переменной линейной части САУ, т.е.:

   .

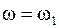Принято обозначение:     , отсюда  .

Уравнение преобразования сигнала однозначным нелинейным элементом:

;

Здесь  -  статический коэффициент усиления гармонической линеаризации.

Таким образом, ограничиваясь рассмотрением первой гармоники на выходе нелинейного элемента  при гармоническом сигнале на его входе, заданное нелинейное выражение можно заменить линейным выражением . Такая замена называется гармонической линеаризацией нелинейных зависимостей.

Однозначные характеристики можно представить прямыми линиями с углом наклона, пропорциональным амплитуде входного сигнала (рис.4). Угол наклона при этом характеризует амплитуду только первой гармоники. Поскольку гармонический коэффициент , определяющий угол наклона луча гармонической линеаризации характеристики , зависит от амплитуды входного сигнала A, при различных значениях A наклон лучей будет различным.

. Рис.4. Гармоническая линеаризация однозначной симметричной нелинейной характеристики

В результате гармонической линеаризации получается не чисто линейное звено, как при линеаризации методом малых отклонений, а своеобразное линейное звено, коэффициент усиления которого  зависит от амплитуды входного сигнала. Сохранение этой весьма существенной особенности нелинейных звеньев в коэффициенте при гармонической линеаризации и является тем важным обстоятельством, которое позволяет методами линейной теории определять свойства нелинейных систем.

Выражения для можно записать в операторной форме для однозначных симметричных нелинейных характеристик:

;

Операторная передаточная функция линеаризованного нелинейного звена при гармоническом колебательном процессе для однозначных симметричных характеристик:

;

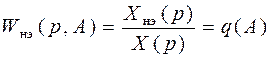Если нелинейная характеристика однозначна и симметрична, то частотная функция нелинейного элемента зависит только от амплитуды A, фаза вектора частотной функции равна нулю, т.е. частотная функция нелинейного элемента является вещественной. Тогда главная операторная передаточная функция разомкнутой нелинейной системы имеет вид:

.