Коэффициент усиления гармонической линеаризации

идеального релейного элемента

Характеристика идеального релейного элемента, однозначная  (без гистерезиса) и симметричная, показана на рис.1,г. Аналитическое выражение для характеристики идеального релейного элемента можно определить на основании выражения:

. (1)

Интеграл выражения (1) практически характеризуют среднее за период значения функций , что может быть использовано для графо-аналитической оценки величины указанного интеграла.

Аналитическое выражение функции  в каждом конкретном случае нелинейной характеристики различно и может быть установлено из графика выходной переменной нелинейного звена при гармоническом сигнале на его входе.

Для идеальной релейной характеристики графики функци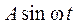й  и показаны на рис. 5, на основании которых построен график , определяющий величину коэффициента гармонической линеаризации усиления .

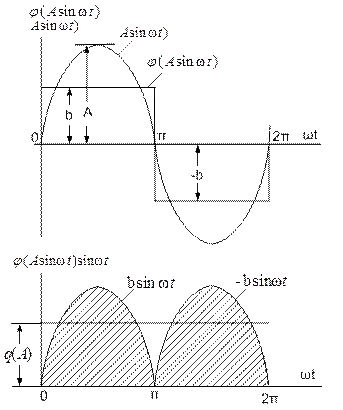
Рис. 5. Графики функций  и 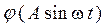гармонической линеаризации характеристики идеального релейного элемента

Коэффициент усиления гармонической линеаризации идеального релейного элемента определяется интегралом:

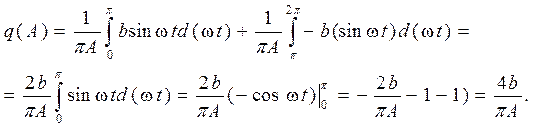
Окончательно коэффициент усиления гармонической линеаризации идеального релейного элемента:

     (2)

3.2Коэффициент усиления гармонической линеаризации

нелинейного элемента с ограничениями

Характеристика нелинейного элемента с ограничениями,однозначная и симметричная, показана на рис.1,б. Графики функций  и  для нелинейного элемента с ограничениямипоказаны на рис.6.

Рис. 6. Графики функций  и гармонической линеаризации характеристики нелинейного элемента с ограничениями

Коэффициент усиления гармонической линеаризации для нелинейного элемента с ограничениями определяется неоднозначно.

При   коэффициент усиления гармонической линеаризации нелинейного элемента равен коэффициенту усиления в пределах линейной части характеристики:

.          (3)

При   коэффициент усиления гармонической линеаризации нелинейного элемента определяется интегральной функцией:

После вычисления интеграла получено:

Здесь   .       

Окончательно коэффициент усиления гармонической линеаризации нелинейного элемента с ограничениями:

. (4)