2020-07-12
112
Фестиваль исследовательских и творческих работ
Учащихся «Портфолио»
"Алгебраические способы решения химических задач "
Автор:
Кимович Кристина Александровна
Россия, Иркутская область,
МОУ " Лицей г.Черемхово"
III курс ЕН
Руководитель:
Гошкадёра Н.А.,
учитель химии
2005 г.
Аннотация
на работу «Алгебраические способы решения задач» Климович Кристины, учащейся МОУ Лицей г. Черемхово, Иркутской обл.
В данной исследовательской работе рассмотрены алгебраические способы решения химических задач с помощью уравнений, систем уравнений и неравенств. Эти способы позволяют упростить алгоритмы решения задач усложнёнными исходными данными. В этой работе реализованы связи между предметами химии и математики; рассмотрены принципы составления алгебраических уравнений и неравенств; приведены развёрнутые решения задач и задачи для самостоятельного решения. Тексты задач взяты из книг, авторов: Н.Е. Кузьменко (проф. химического факультета МГУ), В.В. Ерёмина (доцент химического факультета МГУ), которые были включены билеты на вступительные экзамены в МГУ.
|
|
|
Работа будет полезна учащимся лицеев, гимназий, будущим абитуриентам для подготовки к вступительным экзаменам в ВУЗы.
Учитель химии: Гошкадёра Наталья Анатольевна.
Содержание:
I. Введение……………………………………………………………. 4 стр.
II. Основная часть……………………………………………….. 5-19 стр.
1) Вычисление состава соединений, смесей; выведение формул соединений………………………………………………. … 5-8 стр.
2) Задачи на газовые законы. Определение количественных отношений в газах…………………………………………… 9-13 стр.
3) Решение задач по химическим уравнениям……………….14-19 стр.
III. Задачи для самостоятельного решения…………………………… 20-21 стр.
IV. Заключение ……………………………………………………………… 22 стр.
V. Библиография………………………………………………………………23 стр.
I. Введение.
При изучении химии широко используется решение задач. В данной исследовательской работе рассмотрены способы решения химических задач с помощью методов алгебры: уравнений, систем уравнений, неравенств. Эти приемы позволяют упростить алгоритмы решения задач с усложненными исходными данными. Работа содержит общие положения, касающиеся способов решения расчетных задач. В каждом из следующих разделов рассмотрены принципы составления алгебраических уравнений для задач разных типов, приведены развернутые решения задач и задачи для самостоятельного решения. Широкое применение математики при решении химических задач способствует формированию у учащихся осознанного стремления к применению математических знаний на практике и реализации межпредметных связей между науками химией и математикой.
|
|
|
Алгебраические способы решения задач незаменимы, если задача сложна и ее нельзя решить одной - двумя пропорциями. Именно в этом случае удобно воспользоваться другими методами алгебры, чаще всего линейными уравнениями и неравенствами. Решение задач можно свести к двум этапам: составлению уравнения (системы уравнений) по условию задачи и решению полученного уравнения.
II. Основная часть.
Вычисление состава соединений, смесей, выведение формул соединений.
При решении химических задач часто возникает потребность проводить вычисления для нахождения соотношений составных частей в различных объектах. В качестве последних можно рассматривать химические соединения, смеси веществ, сплавы. Задачи этого типа приходиться решать не только химикам, но и представителям самых разнообразных профессий – агрономам, врачам, металлургам, геологам и т. д.
В задачах обычно рассматриваются объекты, которые состоят из компонентов. Количественный состав объектов удобно выражать в долях, которые составляют компоненты по отношению к целому объекту. Употребляют массовую, объемную и молярную доли. Массовая доля w (X 
) i-го компонента, входящего в состав объекта, равна отношению массы этого компонента m (X ) к массе объекта m (об) и выражается в долях единицы или в процентах:
W (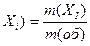
, или w( 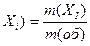100 %
Массу компонента в объекте вычисляют, умножив массу объекта на массовую долю компонента в нем: m(x) = m (об) ∙ w (x)
Так, зная химический состав соединений, т. е. их формулы и молярные массы, можно вычислять массовые доли элементов в этих соединениях. И наоборот, зная массовые доли элементов в соединениях, можно находить молекулярную формулу соединения.
Ниже приведены примеры решения отдельных задач. Все они принадлежат к одному типу, поэтому алгоритмы их решения идентичны. В преобладающем большинстве случаев ход решения строится так: обозначаем буквами неизвестные величины и формулируем их физический смысл; словесно формулируем смысл уравнений и неравенств, которые затем записываем с помощью символов; подставляем числовые значения; решаем систему уравнений и неравенств и даем ответ.
Задача № 1. Вывести формулу вещества с молярной массой 123 г/моль, если состав его, выраженный в массовых долях, следующий: углерод 58,5 %, водород 4,1 %, азот 11,4 %, кислород 26,0 %
Решение: Формулу соединения условно можно записать Cx H y Nz Ot.
Искомые величины – числа атомов в молекуле (индексы в данной формуле- x, y, z, t).
Массовые доли химических элементов в данном веществе можно выразить:
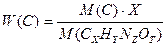W (N) = 
W (H) =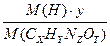 
W (O) =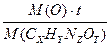 
Составим уравнения, учитывая, что произведение молярной массы соединения на массовую долю данного элемента, входящего в его состав, равно молярной массе элемента, умноженной на его индекс в формуле соединения.
Решим каждое уравнение:
М (Cx Hy Nz Ot) ∙ w (C) = x∙ M (C) 123∙0,585 = 12 х, х = 6
М (Cx Hy Nz Ot) ∙w (H) = y ∙ M (H) 123 ∙ 0. 041 = у у = 5
|
|
|
М (Cx Hy Nz Ot ) ∙ w (N) = z ∙ M (N) 123 ∙ 0, 114 = 14 z z = 1
M (Cx Hy Nz Ot ) ∙ w (O) = t∙ M (O) 123∙ 0,26 = 16t, t=2
Ответ: формула соединения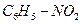 
(нитробензол).
Задача № 2. В кристаллогидрате сульфата марганца (II) массовая доля марганца равна
0, 268. Определить количество вещества воды, приходящееся на 1 моль кристаллогидрата. Написать формулу соли.
Решение: Рассматриваемым объектом является 1 моль кристаллогидрата сульфата марганца (II). Его формулу условно запишем 
, где n- искомая величина.
Составим уравнение, учитывая, что массовая доля марганца в кристаллогидрате равна отношению молярных масс марганца и данного кристаллогидрата:
W (Mn) =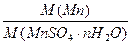 
.
Подставляя в уравнение вместо символов их числовые значения, получим: 0,268 = 
. Решая уравнение, найдём n = 3.
Ответ: 1 моль кристаллогидрата сульфата марганца (II) содержит 3 моль воды. Формула соли - 
.
Задача № 3. При полном сгорании 3,1 г органического вещества (М= 93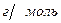 
) образовалось 8, 8 г оксида углерода (IV), 2,1 г воды и выделилось 0,47 г азота. Написать формулу вещества.
Решение: В общем виде соединение можно представить формулой 
, где х, у, z и t- искомые величины.
Составим уравнения, учитывая следующее:
1) масса углерода в сгоревшем веществе и в образовавшемся оксиде углерода
(IV) равны:
m (Cx Hy Nz Ot) 
или 3,1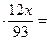 
88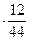 
, откуда х=6;
1) массы водорода в сгоревшем веществе и в образовавшейся воде равны:
m (CxHyNzOt)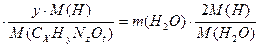 
или 3,1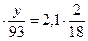 
, откуда у=7;
2) масса азота в 3,1 г соединения равна 0,47 г:
m () 
, 3,1 
,
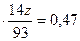откуда z=1;
3) молярная масса соединения равна сумме молярных масс каждого элемента, умноженных на соответствующие индексы в формуле:
М () = х 
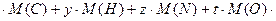, или
93=6 
, откуда t =0.
Ответ: формула соединения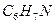 
(анилин).
Задача № 4. Массовая доля серебра в соли предельной одноосновной органической кислоты составляет 70,59 %. Написать молекулярную формулу этой кислоты, если известно, что она состоит из углерода, водорода и кислорода.
Решение: Запишем химические формулы кислот и её соли в условном виде: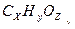 
и Аg 
.Индексы х, у и z-искомые величины.
|
|
|
Выражая молярную массу соли серебра через молярные массы составляющих её атомов, получим:
М (Аg 
) = х 
Составим уравнение, учитывая, что произведение молярной массы соли на массовую долю в ней серебра равно молярной массе серебра:
М (Аg ) 
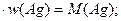
(107+12х+у+16z)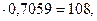 
откуда 12х + у + 16z = 46.
По условию задачи одноосновная предельная органическая кислота имеет общую формулу 
, или,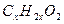 
. Отсюда у =2х, z = 2.
Искомые числа х и у одновременно удовлетворяют двум уравнениям:
12х +у +16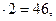 
2х = у
Решая систему уравнений, получим х = 1, у = 2. Следовательно, формула кислоты - 
, или НСООН.
Ответ: Формула кислоты - НСООН.
Задача № 5. После полного термического разложения 2,0 г смеси карбонатов кальция и стронция получили 1,23 г смеси оксидов этих металлов. Оксид углерода (IV) улетучился. Вычислить массу карбоната стронция в исходной смеси.
Решение: Запишем уравнение реакции:
x y
SrC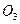 
→ SrO + C 
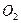(I)
148 г 104 г
2-х 1,23-у
CaC 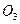→ CaO + C 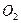(II)
100 г 56 г
Искомую величину- массу карбоната стронция в смеси обозначим через х: m (SrC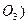 
= x. Тогда масса карбоната кальция будет равна m (CaC 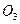) = 2-x, а масса выделившегося оксида углерода (IV) составит m (C 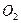) = (2-1,23) г = 0,77 г.
Составим уравнение, учитывая, что масса углерода в исходной смеси карбонатов металлов равна массе углерода в выделившемся оксиде углерода (IV):
m (CaC )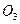 
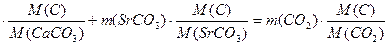
Подставляя числовые значения, получим:
(2-х)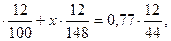 
откуда х=0,75.
Ответ: масса карбоната стронция равна 0,75 г.
Задача № 6. Рассчитать массовые доли компонентов смеси, состоящей из гидрата карбоната аммония, карбоната калия и гидрофосфата аммония, если известно, что из 38,4 г этой смеси получили 8,8 г углекислого газа и 6,8 г аммиака.
Решение:
М (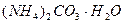
) = 114 г/моль
М (
) = 138 г/моль
М (
) = 132 г/моль
Пусть в смеси х моль 
, у моль 
и z моль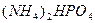 
, тогда
114х + 138у + 132z = 38,4
Из х моль гидрата карбоната аммония можно получить 2х моль аммиака и
х моль углекислого газа:
х 2х х
→ 2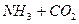 
Аналогично,
у у z 2z
→ 
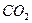
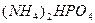→ 2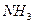 
n (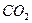) = 8,8/44 = 0,2 моль х + у = 0,2
n (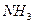) = 6,8/ 17= 0,4 моль 2х+2z =0,4
Решая систему уравнений
114х + 138у + 132z = 38,4
х + у = 0,2
2х+2z =0,4
находим х = у = z = 0,1 моль
w (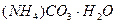
) = 
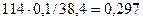
w () = 
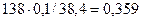
w ((NH4)HPO4 = 
Ответ: w (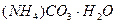) = 29,7 %, w() = 35,9 %,
w () = 34,4 %.
