2020-07-12
755
В газах.
Расчёты масс, количеств веществ и объёмов газов обычно проводят с помощью алгебраических уравнений, как правило, на основе закона Авогадро. Рассмотрим некоторые особенности составления таких уравнений.
Иногда в задачах требуется произвести вычисления с газами, при смешении которых не происходит химического взаимодействия, а образуется смесь исходных газов. В таких случаях при составлении алгебраических уравнений учитывают, что масса газовой смеси равна сумме масс газов смеси. В уравнении массу каждого газа, а также смеси представляют как произведение количества вещества газа на его молярную массу: m = n* M. В отдельных задачах при составлении уравнений принимают во внимание, что количество вещества в газовой смеси равно сумме количеств веществ газов, которые были смешаны.
Если в условии задачи задана относительная плотность D некоторого газа, имеющего молярную массу М (х), по другому газу, имеющего молярную массу М (а), то можно использовать существующую зависимость между этими величинами: D = М (х) / М (а) – выражать молярную массу газа М (х) в виде произведения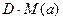 
.
Во многих задачах рассматриваются газы, которые при смешении реагируют между собой, образуя газообразные продукты реакции. В таких случаях при составлении алгебраических уравнений учитывают, что объёмы участвующих в реакции газов относятся как коэффициенты перед формулами соединений в уравнении химической реакции. Причём объёмы газов должны быть взяты при одинаковой температуре и давлении. В алгебраических уравнениях отношение объёмов реагирующих газов иногда удобно заменять отношением количеств веществ газов.
В процессе решения задач, касающихся газов, иногда полезно использовать информацию, которую можно представить в виде неравенств. Последние иногда непосредственно следуют из условия задачи. Однако в ряде случаев их можно составлять на основе известных свойств газов. Например, для любого газа относительная плотность по водороду больше единицы: DH > 1; средняя молярная масса газа, состоящего из молекул различных соединений, находится в пределах значений молярных масс этих соединений: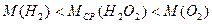 
и т. п.
Иногда в условиях задач объём газа даётся не при нормальных, а при каких-то других условиях. В этом случае, как обычно говорят, нужно привести объём к нормальным условиям. Для этого проще всего воспользоваться объединённым газовым законом, который математически выражается так:
.
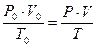Где V0 – объём газа при н.у., т.е. при нормальной температуре T0 = 273 K и при нормальном давлении P0 =101325 Па; V- объём газа при данной температуре T и данном давлении P.
Значение молярной массы газа, а также число молей газа можно найти при использовании уравнения Клапейрона - Менделеева:
PV=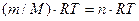 
Где P - давление газа, V- объём системы, m – масса газа, Т- абсолютная температура, R- универсальная газовая постоянная: R= 8,31 Дж / (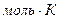
).
При расчётах газовых реакций нет необходимости определять число молей веществ, а достаточно пользоваться их объёмами. Из закона Авогадро и основного закона стехиометрии вытекает следующее следствие отношение объёмов газов, вступающих в реакцию, равно отношению коэффициентов в уравнении реакции. Это утверждение называется законом объёмных отношении Гей-Люссака.
Задача № 1. Какой объём (н.у.) озонированного кислорода с молярной долей озона 24 % требуется для сжигания 11,2 л водорода.
Решение: Реакциям горения водорода отвечают уравнения:
2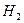 
+ 
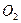= 2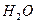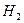 
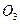3 + 
= 3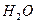
Искомая величина V (смеси) – объём озонированного кислорода, необходимый для сжигания 11,2 л водорода. Составим уравнения, учитывая, что количество вещества водорода равно сумме удвоенного количества кислорода и утроенного количества вещества озона.
n (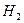) = 2n (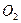)+ 3n (),
,
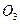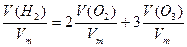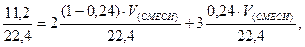
Откуда V (смеси) =5 л.
Ответ: 5 л озонированного кислорода.
Задача № 2. К 30 л смеси, состоящей из этана и аммиака добавили 10 л хлороводорода, после чего плотность паров газовой смеси по воздуху стало равной 0,945. Вычислить объёмные доли газов в исходной смеси.
Решение:
При добавлении хлороводорода происходит реакция
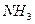+ HCl →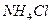 
с образованием твёрдого .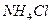
Конечная газовая смесь имеет среднюю молярную массу
Мср =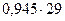 
= 27,4 г/ моль
и состоит из этана (М= 30 г/ моль) и аммиака (М= 17 г/ моль). Это означает, что аммиак в реакции - в избытке. Если бы в избытке был хлороводород, то в конечной смеси вместо аммиака был хлороводород, и средняя молярная масса была бы больше 30 г/ моль.
Пусть в исходной смеси было х л аммиака и у л этана, тогда в конечной смеси содержатся
(х - 10) л аммиака и у л этана. Значения объёма исходной смеси и молярной массы конечной смеси дают систему двух уравнений для х и у:
х + у = 30
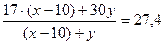
откуда следует х=14 л, у=16 л.
φ (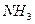) = 14/30 = 0,47, φ (
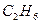) = 16/30 = 0,53.
Ответ: 47 % 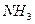, 53 % .
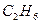Задача № 3. Смесь паров пропина и изомерных монохлоралкенов при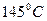 
и давлении 96,5 кПа занимает объём 18 л и при сжигании в избытке кислорода образует 18 г воды. Вывести формулы монохлоралкенов. Вычислить объём 1,7 % раствора нитрата серебра (плотность 1,01 г/мл), который может прореагировать с продуктами сжигания исходной смеси, если известно, что её плотность по воздуху 1,757.
Решение: Общая формула монохлоралкенов -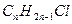 
.
Сгорание компонентов смеси происходит по уравнениям:
х 2х
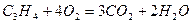
у (n -1)y
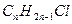+ (1.5 n-0.5) 
.
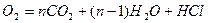Пусть в смеси было х моль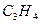 
(М = 40) моль, y моль 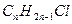(М = 14n+34).
Общее количествo веществa в газовой смеси: n = PV/RT = 96.5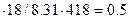 
моль. Средняя молярная масса смеси равна М=29 
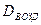= 50.95 г/моль.
Отсюда масса 0.5 моль смеси составляет m = 50.95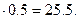 
При сгорании х моль 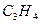образуется 2х моль воды, а при сгорании у моль 
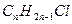образуется у 
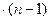моль воды.
Всего получено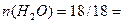 
1 моль.
Таким образом, можно составить систему из трёх уравнений:
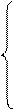
x + у = 0.5
40х + (14n + 34.5) y = 25.5
2x + y (n-1) = 1
Решение этой системы даёт х = 0.35 моль, у = 0.15 моль, n = 3.
Неизвестные монохлоралкены имеют молекулярную формулу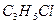 
.
В смеси содержалось 0.15 моль 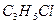, при сгорании которых по уравнению
0,15 моль 0,15 моль
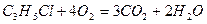+ HCl
образовалось 0,15 моль HCl.
В реакцию
0,15 0,15
HCl +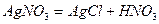 
Вступило 0.15 моль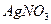 
.
m (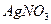) = 0.15 
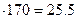г.
w (AgNO3) =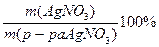 
m (р-ра 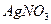) = 25.5/0.017= 1500 г
V (р-ра 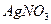) = 1500/1.01= 1485 мл.
Ответ: 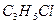, 1485 мл раствора .
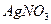Задача № 4. К 30 литрам смеси, состоящей из аргона и этиламина, добавили 20 литров бромоводорода, после чего плотность газовой смеси по воздуху равна 1,814. Вычислить объёмные доли газов в исходной смеси.
Решение: Пусть в исходной смеси содержалось х л Ar и у л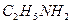 
, тогда
х + у = 30
При добавлении бромоводорода происходит его реакция с этиламином и образуется твёрдое вещество – бромид этиламмония.
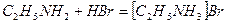
Средняя молярная масса оставшейся газовой смеси равна
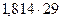=52,6 г/моль
Это означает, что в газовой смеси находятся Ar и HBr (если бы в смеси остались Ar и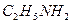 
, то 40 < МСР < 45).
Пусть объём аргона в оставшейся газовой смеси - х л V (Ar) = x, тогда
V (HBr) = 20-y.
МСР =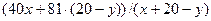 
= 52,6
Решим систему уравнений:
х + у = 30
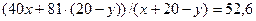
находим: х = 18, у =12.
Объёмные доли равны w (Ar) = 18/ 30 = 0,6 (или 60 %)
W (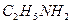) = 12/ 30 = 0,4 (или 40 %).
Ответ: 60 % Ar, 40 % .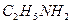
Задача № 5. Рассчитайте массовую долю более лёгкого газа в смеси состоящей из аммиака и азота имеющий плотность 1,03 г/л при давлении 90 кПа и температуре 263 К.
Решение: Возьмём 1 моль смеси, которая содержит х моль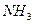 
и у моль 
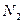, то есть
х + у =1
Средняя молярная масса смеси газов может быть рассчитана с помощью уравнения Клайперона - Менделеева: PV =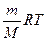 
; ρ =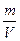 
; M = ρ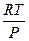 
M =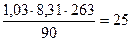 
г/моль 
В таком случае масса 1 моля смеси равна 25 г:
17х + 28 у =25
Решая систему уравнений:
х + у =1
17х + 28 у =25
находим х = 0,273 моль, у = 0,727 моль
w (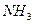) = 17 
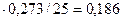(18,6 %)
Ответ: w (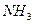) = 18,6 %.
Задача № 5. При нормальных условиях 12 л газовой смеси, состоящей из аммиака и оксида углерода (IV), имеют массу 18 г. Сколько литров каждого из газов содержит
смесь?
Решение: Стандартный способ решения расчётных задач на установление состава смеси – обозначить количества веществ через неизвестные переменные и составить для них систему уравнений.
Пусть n (NH3) = х моль, n (CO2) = у моль. Массы газов равны: m (NH3) = x 17 г,
m (CO2) = у 44 г. Общее число молей газов в смеси равно 12/22,4 = 0,536 моль.
Составим систему уравнение:
х + у = 0,536 (количество смеси),
17x + 44y = 18 (масса смеси)
Решая систему, находим: х = 0,207 л, у =0,329 л. Объёмы газов равны:
Ответ: 4,64 л NH3, 7,36 л. CO2.
