Форматирование с целью передачи – это преобразование исходной информации в цифровые сигналы.
Сигнал называется узкополосным (УПС), если ширина его спектра значительно меньше средней частоты: 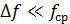 . Типичными представителями УПС являются модулированные радиосигналы.
. Типичными представителями УПС являются модулированные радиосигналы.
Операция дискретизации – осуществляет преобразование аналоговых сигналов (функций), непрерывных по аргументу, в функции мгновенных значений сигналов по дискретному аргументу.
Операция восстановления аналогового сигнала из его дискретного представления обратна операции дискретизации и представляет, по существу, интерполяцию данных.
Теорема Котельникова: если аналоговый сигнал 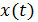 имеет конечный (ограниченный по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своим отсчётам, взятым с частотой, большей или равной удвоенной максимальной частоте
имеет конечный (ограниченный по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своим отсчётам, взятым с частотой, большей или равной удвоенной максимальной частоте 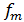 :
:
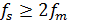
 – частота дискретизации;
– частота дискретизации;
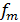 – максимальная частота, которой ограничен спектр реального сигнала.
– максимальная частота, которой ограничен спектр реального сигнала.
Отсчет – мгновенное значение, взятое через определенный интервал времени.
Частота дискретизации – частота взятия отсчетов непрерывного во времени сигнала при его дискретизации.
Условие задачи:
Определите максимальную частоту дискретизации, необходимую для выборки и точного восстановления сигнала 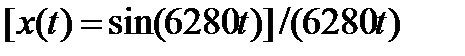 .
.
Дано:
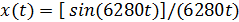 ,
,
где x(t) – функция отсчета
Найти:
Максимальную частоту дискретизации fs -?
Решение:
1) Для решения данной задачи используем теорему Котельникова (теорема отсчётов). В соответствии с теоремой Котельникова точное восстановление сигнала возможно, только если частота дискретизации выше, чем удвоенная максимальная частота в спектре сигнала. Данная теорема выражается по формуле приведенной ниже:
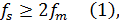
где  – частота дискретизации;
– частота дискретизации;
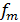 – максимальная частота.
– максимальная частота.
Теорема отсчётов гласит, что при некоторых ограничивающих условиях, функция x(t) может быть восстановлена из её дискретизации, согласно интерполяционной формуле, представленной ниже:
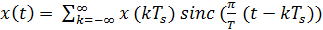 (2)
(2)
где 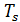 – период дискретизации,
– период дискретизации, 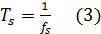 ;
;
fs – частота дискретизации;
x(k 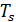 ) - мгновенные значения данного ряда (дискретные отсчёты сигнала);
) - мгновенные значения данного ряда (дискретные отсчёты сигнала);
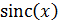 - нормированная
- нормированная 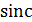 - функция, в цифровой обработке сигналов и в теории связи
- функция, в цифровой обработке сигналов и в теории связи 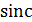 - функция, применяемая для восстановления аналогового сигнала по его отсчётам. Нормированная функция
- функция, применяемая для восстановления аналогового сигнала по его отсчётам. Нормированная функция 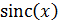 определяется по следующей формуле:
определяется по следующей формуле:
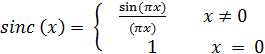 (4)
(4)
2)Для дальнейшего решения задачи нам следует преобразовать данную в условии функцию отсчета 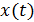 в нормированную
в нормированную 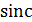 – функцию. Для этого используем свойство нормированной функции, представленное в формуле (4):
– функцию. Для этого используем свойство нормированной функции, представленное в формуле (4):
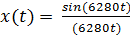 ,
,
выделяем 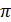 из значения 6280t и получаем:
из значения 6280t и получаем:
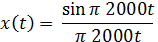
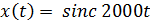
3) Используяинтерполяционную формулу (2) и подставляя выражения полученные выше, находим 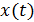 :
:
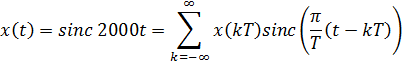
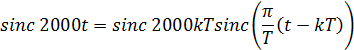
4)При 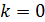 функция отсчетов имеет максимальное значение при
функция отсчетов имеет максимальное значение при 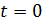 , согласно формуле (4)
, согласно формуле (4) 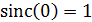 , отсюда следует:
, отсюда следует:
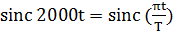
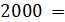

T = 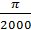
5)Вычисляем частоту дискретизации по формуле (3):
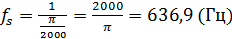
Ответ: максимальная частота дискретизации 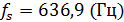 .
.
Заключение
Для решения данной задачи мы использовали теорему Котельникова (теорема отсчётов). В соответствии с теоремой Котельникова точное восстановление сигнала возможно, только если частота дискретизации выше, чем удвоенная максимальная частота в спектре сигнала. Данная теорема выражается по формуле приведенной ниже:
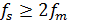
где  – частота дискретизации;
– частота дискретизации;
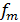 – максимальная частота.
– максимальная частота.
Также в ходе решения мы полагались на интерполяционную формулу, представленную ниже:
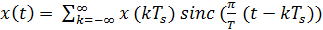
 2020-07-12
2020-07-12 213
213








