Тема 6. Канальное кодирование: часть 1. Вариант 7

Канальное кодирование (channel coding) представляет собой класс преобразований сигнала, выполняемых для повышения качества связи. В результате этого сигнал становится менее уязвим к таким эффектам ухудшения качества передачи, как шум, помехи и замирание. Канальное кодирование можно считать способом при­ведения параметров системы к желаемому компромиссу (т.е. соотношению между достоверностью передачи и шириной полосы пропускания или мощностью и ши­риной полосы пропускания).

Когерентное детектирование – способ детектирования, основанный на взаимной зависимости принимаемого сигнала и являющийся его точной копией сигнала местного источника.

Систематический линейный блочный код (n, k) — это такое отображение n-мерного вектора сообщения в n-мерное кодовое слово, что часть генерируемой последовательности совмещается с k символами сообщения. Остальные (n - k) бит — это биты четности.

Минимальное расстояние d_min соответствует наименьшему из множества расстояний между нулевым кодовым сло­вом и всеми остальными кодовыми словами.

Способность кода к исправлению ошибок t определяется, как максимальное число гарантированно исправимых ошибок на кодовое слово.

Возмож­ность определения наличия ошибки: блочный код с минимальным расстоянием d_min гарантирует обнаружение всех ошибоч­ных комбинаций, содержащих d_min - 1 или меньшее число ошибочных бит.

Возможность кода при коррекции стираний для данной длины блока – комбинация стертых символов.

Условие задачи:

Минимальное расстояние для конкретного линейного блочного кода равно 11. Найдите максимальные возможности кода при исправлении ошибок, максимальные возможности при обнаружении ошибок и максимальные возможности этого кода при коррекции стираний для данной длины блока.

Дано:

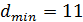, где  – минимальное расстояние

для конкретного линейного блочного кода

Найти:

1) Способность кода к исправлению ошибок   -?

2) Возможность кода к определению наличия ошибки   -?

3) Возможность кода при коррекции стираний для данной длины блока  -?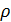

Решение:

1) Способность кода к исправлению ошибок   определяется, как максимальное число гарантированно исправимых ошибок на кодовое слово, и выражается формулой приведенной ниже:

где   минимальное расстояние, которое соответствует наименьшему из множества расстояний между нулевым кодовым сло­вом и всеми остальными кодовыми словами.

Используя формулу (1) вычисляем способность кода к исправлению ошибок:

 

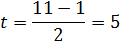
2) Возмож­ность определения наличия ошибки определяется по формуле приведенной ниже:

где блочный код с минимальным расстоянием 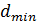гарантирует обнаружение всех ошибоч­ных комбинаций, содержащих  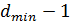или меньшее число ошибочных бит.

Вычисляем возможность определения наличия ошибки по формуле (2):

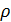3) Если минимальное расстояние кода равно , любая комбинация из  или меньшего числа стертых симво­лов может быть исправлена по формуле приведенной ниже:

Исходя из формулы (3) возможность кода при коррекции стираний для данной длины блока определяется по следующей формуле:

Используя формулу (4) вычисляем возможность кода при коррекции стираний для данной длины блока:

 

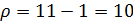
Ответ:

1) способность кода к исправлению ошибок ;

2) возможность кода к определению наличия ошибки ;

3) возможность кода при коррекции стираний для данной длины блока .

Заключение

Способность кода к исправлению ошибок t определяется, как максимальное число гарантированно исправимых ошибок на кодовое слово, и находили по формуле:

Возмож­ность определения наличия ошибки определяли с помощью следующего выражения:

Если минимальное расстояние кода равно d_min, любая комбинация из ρ или меньшего числа стертых симво­лов может быть исправлена при следующем условии.