Ортогональное и центральное проектирование ортогональное проектирование

Параллельное проектирование в направлении прямой, перпендикулярной плоскости проектирования.

Так как ортогональное проектирования является частным случаем параллельного проектирования, то для него верны все свойства параллельного проектирования.

Для изображения прямоугольного параллелепипеда или куба в ортогональной проекции важно понять, куда переходят рёбра прямого трёхгранного угла при ортогональном проектировании.

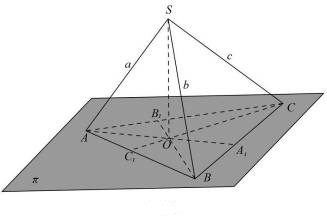
Рисунок 10 – Изображение прямоугольного параллелепипеда

Пусть дан прямой трёхгранный угол с вершиной S и рёбрами a, b, c. Плоскость пересекает эти ребра в точках A, B и C (рис. 10). Обозначим через O ортогональную проекцию вершины S на плоскость. Тогда прямые AO, BO и CO будут ортогональными проекциями прямых SA, SB и SC соответственно. Докажем, что точка O является ортоцентром треугольника ABC.

Доказательство. По условию, прямая SC перпендикулярна прямым SA и SB. Следовательно, она перпендикулярна плоскости SAB.

Прямая AB лежит в этой плоскости. Значит, она перпендикулярна прямой SC. Прямая CO является ортогональной проекцией SC, значит, по теореме о трёх перпендикулярах, перпендикулярна AB. Таким образом, прямая CO содержит высоту треугольника ABC. Аналогично доказывается, что прямые AO и BO содержат соответствующие высоты треугольника ABC. Итак, точка O является ортоцентром треугольника ABC.

Кроме параллельного и ортогонального проектирования, которые широко применяются в геометрии для изображения пространственных фигур, большое значение имеет и, так называемое, центральное проектирование, которое нашло применение в фотографии, живописи и т. д. Это обусловлено тем, что восприятие человеком окружающих предметов с помощью зрения осуществляется как раз непосредственно по законам центрального проектирования.

Центральное проектирование, или, говоря иначе, перспектива, в качестве науки образовалась ещё в Древней Греции. Самые первые упоминания о перспективе встречаются в работах Эсхила (525-456 гг. до н. э.).

Леонардо да Винчи в своём произведении «Трактат о живописи» выделил три основные части перспективы:

- линейная перспектива, она занимается изучением законов построения уменьшения фигур по мере удаления их от наблюдателя;

- воздушная и цветовая перспектива, которая трактует изменение цвета предметов в зависимости от их расстояния до наблюдателя и влияния слоя воздуха на насыщенность и локальность цвета;

- перспектива чёткости очертания формы предмета, которая занимается анализом изменений степени отчётливости границ фигур и контраста света и тени на них, по мере удаления их в глубину пространства, изображаемого на картине.

Два последних раздела не получили дальнейшего теоретического развития из-за большой сложности исследования поставленной проблемы.

Первый же раздел развился в точную науку - линейную перспективу, позднее ставшей одной из составных частей в начертательной геометрии.

Обозначим р - некоторую плоскость, и пусть S - не принадлежащая ей точка, центр проектирования (рис. 11). Проведём прямую a, проходящую через точку A пространства и соединяющую эту точку с точкой S. Точка пересечения этой прямой с плоскостью р называется центральной проекцией точки A на плоскость р.

Рисунок 11 – Центральная проекция многоугольника

Обозначим её A'. Соответствие, при котором точкам A пространства сопоставляются их центральные проекции A', называется центральным проектированием, или перспективой.

Следует заметить, что вовсе не для любой точки пространства определена её центральная проекция. Если рассмотреть случай, когда прямая a и плоскость р параллельны, то точка A на эту плоскость проекции не имеет.

Если мы рассмотрим некоторую фигуру Ц в пространстве, то проекции всех её точек на плоскость р образуют фигуру Ц', которая называется центральной проекцией фигуры Ц на плоскость р.

Теорема. Если плоская фигура F расположена в плоскости б, параллельной плоскости проектирования р, то её центральной проекцией будет фигура F', подобная F, причём коэффициент подобия k будет равен отношению расстояний от центра S до плоскостей р и б (рис. 12).

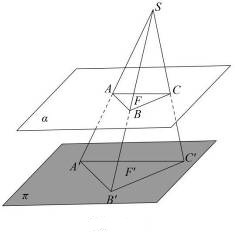
Рисунок 12 – Центральная проекция двух фигур

Доказательство. Зададим преобразование фигуры F в фигуру F', сопоставляя каждой точке фигуры F её центральную проекцию. Через центр S перпендикулярно плоскости р проведём прямую. Исходя из того, что по условию плоскости р и б параллельны, эта прямая будет перпендикулярна и плоскости б. Обозначим точки пересечения этой прямой с плоскостями б и р буквами C и C'

соответственно. Для точек A и B фигуры F на плоскости б рассмотрим их центральные проекции соответственно A' и B'. Образовались треугольники ABS, A'B'S и ACS, A'C'S. Заметим, что эти треугольники подобны, и коэффициент подобия k равен отношению длин соответственных сторон SC: SC'.

Таким образом, определённое преобразование фигуры F в фигуру F' изменяет расстояние между точками в одно и то же число раз. Значит, можно сделать вывод, что фигуры F и F' подобны.

Выясним, в какую фигуру при центральном проектировании переходит прямая.

Пусть прямая a пересекает плоскость проектирования р, а центр проектирования S не принадлежит прямой a. Найдём проекцию этой прямой на плоскость р. Через прямую a и центр проектирования S проведём плоскость б, обозначим линию её пересечения с плоскостью р через a' (рис. 13).

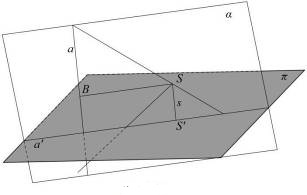
Рисунок 13 – Нахождение проекции через плоскость

Через точку S, принадлежащую плоскости б, проведём прямую s, параллельную прямой а, и обозначим точку её пересечения с прямой a' через S'. Заметим, что все точки прямой a, кроме точки B, имеют проекции на плоскость р. Для точки В, поскольку SB параллельна плоскости р, проекции не существует. Значит, прямая а', без точки S', является искомой проекцией прямой a (без точки B) на плоскость р.

Выясним, в какие фигуры могут переходить параллельные прямые при центральном проектировании. Мы знаем, что при параллельном проектировании параллельные прямые переходят или в параллельные прямые, или в одну прямую, или в две точки, что определяется расположением этих прямых относительно направления проектирования. Оказывается, при центральном проектировании параллельные прямые могут переходить и в пересекающиеся прямые.