2020-07-12
772
5.1. Рациональное неравенство — это такой вид неравенства в котором левая и правая части рациональные выражения. В записи имеются только сложение, вычитание, умножение, деление, а также возведение в целую степень.
Задача№13. Решить неравенство 
На первом этапе раскрываем скобки (если они имеются) и переносим все неизвестные переменные влево, а числа вправо 
Приведем подобные слагаемые слева и справа, получим 
Разделим все на 4. Так как 4 положительное число, то знак неравенства не меняется. Если же мы будем умножать на число, меньше нуля, то знак неравенства необходимо менять на противоположный В нашем случае получим: 
Ответ: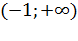 
.
Задача№14. Решить систему неравенств 
; 
; 
Отметим оба получившихся решения на одной прямой.
В ответ записываем ту часть числовой прямой где сошлись оба решения вместе.
Ответ: 
.
5.2. Иррациональное неравенство — это такой вид неравенства, содержащее неизвестное под знаком корня. или возведённое в степень, которую нельзя свести к целому числу.
|
|
|
Задача№15. Решить неравенство 
Область допустимых значений: 
Неравенство будем решать методом интервалов.
1. Вместо знака неравенства запишем знак равенства и решим полученное уравнение 
Так как у нас слева корень четной степени, то здесь получается дополнительная область определения 
Возведем обе части уравнения в квадрат: 
; 
.
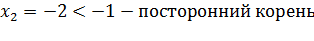2. 
Отмечаем корни на числовой прямой вместе с областью определения неравенства, расставляем знаки на полученных промежутков (проверяем выполнение на промежутке неравенства, если неравенство выполнено ставим плюс, если нет – минус).
Ответ: 
Задача№16. Решить неравенство 
Т.к. как в неравенстве есть квадратный корень, то находим 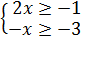ОДЗ: 
; 
; 
ОДЗ: 
.
Решаем неравенство методом интервалов. Для этого выполняем следующее:
1. Вместо знака неравенства запишем знак равенства и решим полученное уравнение 
; 
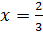
2. Отмечаем корни на числовой прямой вместе с ОДЗ и расставляем знаки на получившихся интервалах
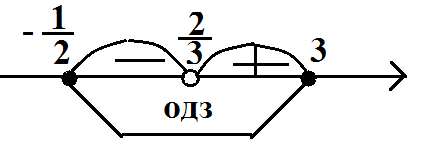Ответ: 
