Тригонометрическое уравнение — это уравнение, содержащее в себе одну или несколько тригонометрических функций.
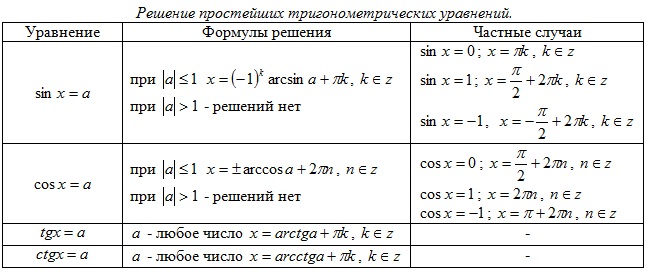
Формулы для решения простейших тригонометрических уравнений
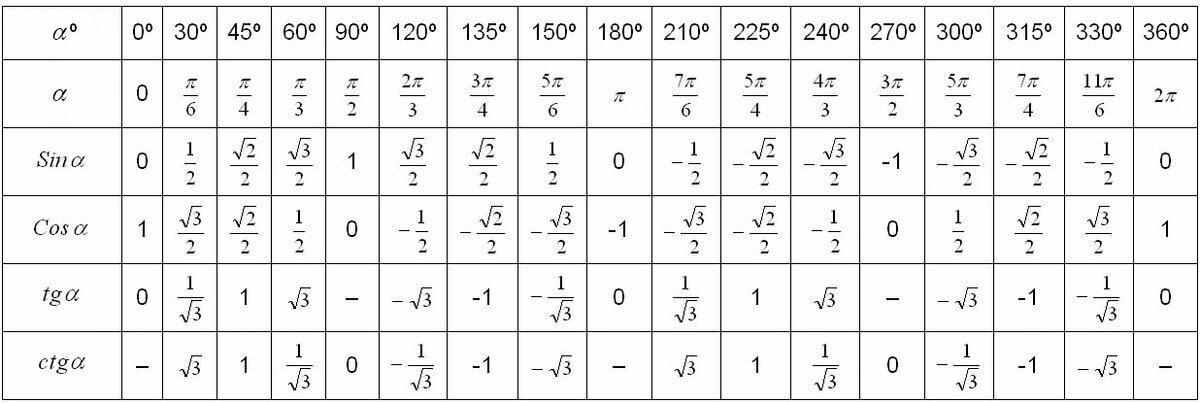
 Также пригодится таблица значений тригонометрических функций
Также пригодится таблица значений тригонометрических функций
Задача№7. Решить уравнение 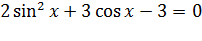
Приведём уравнение к однородному, т.е. к такому, в котором только один вид тригонометрической функции. Из основного тригонометрического тождества можно вывести следующую формулу 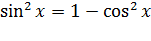 . Подставим ее в уравнение
. Подставим ее в уравнение
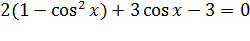 ;
; 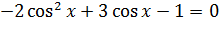
Обе части уравнения умножим на -1, получим 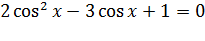
Сделаем замену 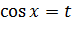 , получим
, получим 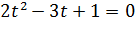
Получили квадратное уравнение, решая его через дискриминант: 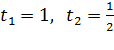
Вернемся к замене. Получаем два простейших тригонометрических уравнения:
1) 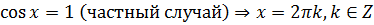
2) 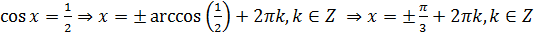
Ответ: 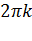 и
и 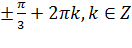 .
.
Задача№8. Решить уравнение 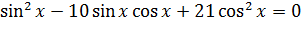
Приводим уравнение к однородному: разделим обе части уравнения на 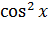 .
.
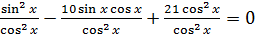
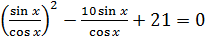
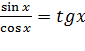 , получим
, получим 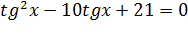
Замена: пусть 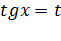 , тогда уравнение примет вид
, тогда уравнение примет вид 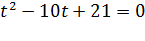
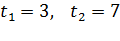
Вернемся к замене. Получаем два простейших тригонометрических уравнения:
1) 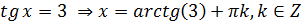
2) 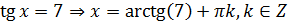
Ответ: 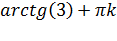 и
и 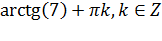 .
.
Задача№9. Решить систему уравнений 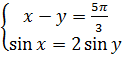
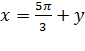 ;
; 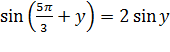
Воспользовавшись формулой синуса суммы, получим
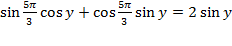 ;
; 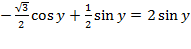 ;
;
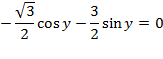
Разделим обе части уравнения на 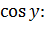
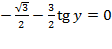 ;
; 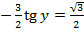 ;
; 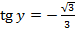
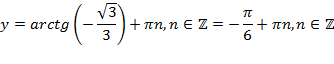
Чтобы найти вторую переменную  подставим найденный
подставим найденный  в выражение
в выражение 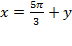 :
:
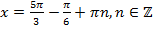
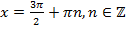 Ответ:
Ответ: 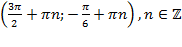 .
.
 2020-07-12
2020-07-12 1069
1069








