2020-07-12
388
Показательное неравенство — это любое неравенство, содержащее в себе показательную функцию, т.е. выражение вида 
.
Задача№17. Решить неравенство 
И левую и правую часть приводим к одному основанию степени 
.
Далее используем правило: если основания степени больше 1, то знак неравенства остается неизменным, если же меньше 1, то знак неравенства необходимо поменять на противоположный. Поэтому имеем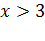 
Ответ: 
.
Задача№18. Решить неравенство 
; 
; 
Решим неравенство методом интервалов. Приравняем к нулю: 
По теореме Виета: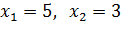 
. Отмечаем их на числовой прямой, ставим знаки.
Ответ: 
.
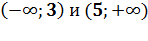Задача№19. Решить неравенство 
Преобразуем неравенство, используя следующие 3 свойства: 
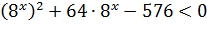
Решаем неравенство методом интервалов.
1. Вместо знака неравенства запишем знак равенства и решим полученное уравнение
Сделаем замену 
. Получим 
и 
Возвращаясь к замене, получим 
2. Отмечаем корни на числовой прямой и расставляем знаки на полученных промежутков (проверяем выполнение на промежутке неравенства, если неравенство выполнено ставим плюс, если нет – минус).
Ответ: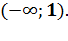 
Решение тригонометрических неравенств.
Задача№20: 
Найдем решение тригонометрического неравенства 
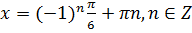
Отметим решение на тригонометрической окружности.Так как неравенство имеет знак «больше или равно», то решение лежит на верхней дуге окружности (относительно решения уравнения).
Ответ: 
.
Задача№21: 
; 
;
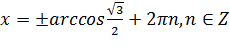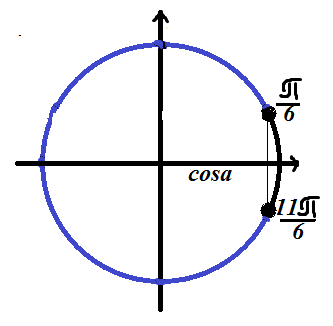
Отметим решение на тригонометрической окружности
Так как неравенство имеет знак «меньше», то решение лежит на дуге окружности, расположенной слева (относительно решения уравнения).
Ответ: 
.
Задача№22: 
Найдем решение тригонометрического неравенства 
; 
,
ОДЗ: 
.
Отметим решение на тригонометрической окружности: решение лежит на дугах окружности, отмеченных синим т.е. x 
