Решение логарифмических неравенств

Логарифмическое неравенство — это любое неравенство, содержащее в себе логарифмическую функцию.

Задача№23. Решить неравенство  

ОДЗ: ;             

Левую и правую часть неравенства приводим к одному основанию логарифма

;

Если основания логарифма больше 1, то знак неравенства остается неизменным, если же меньше 1, то знак неравенства необходимо поменять на противоположный.

 знак неравенства меняем на противоположный ;   

С учетом ОДЗ, ответ: .

Задача№24. Решить неравенство

ОДЗ:

;

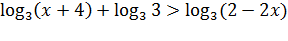Так как основание логарифма 3 больше 1, то знак неравенства не меняем

; 

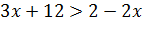С учетом ОДЗ, ответ: .

Литература

1. Алимов Ш.А., Колягин Ю.М., Ткачева М.В. и др. Математика: алгебра и начала математического анализа. 10-11классы: учебник для общеобразовательных организаций: базовый и углубленный уровни/ Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др. 3-е изд.- М.: Просвещение, 2016.-463с.: ил.

2. Башмаков М.И. Математика: учебник / М.И.Башмаков.- М.: КНОРУС, 2017.-394с. -(Начальное и среднее профессиональное образование).

Дополнительная литература

1. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов/ В. Е. Гмурман. - 9-е изд., стер. - М.: Высш. шк., 2004. — 404 с: ил.

Задание

1. Прорешать задачи приведенные в данном практическом занятии.

2. Выполнить упражнения: литература [1] №223, №340, №359, №576.

3. Переслать сканы выполненного задания личным сообщением на https://vk.com/id587846845 или на электронную почту annokhonchenko@rambler.ru