Решение некоторых уравнений высших степеней

Почему уравнение не имеет решений

Вынесем из выражения общий множитель :

Представим выражение следующим образом:

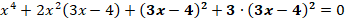
В первых трех слагаемых видим полный квадрат, свернем его по формуле :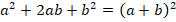

Каждое из полученных слагаемых – неотрицательная величина. Их сумма может быть равна нулю только в том случае, если каждое из них равно нулю:

Второе слагаемое равно нулю только при :

Но при первое слагаемое равно , а не нулю. Таким образом, сумма этих двух слагаемых не равна нулю ни при каких действительных значениях :

Уравнение не имеет решений.

Получаем ответ:

Ответ: .

Свойства степенных функций

Отметим, что исходное уравнение получилось эквивалентно уравнению . Или, еще можно сказать, уравнение эквивалентно уравнению . То есть если равны кубы выражений, то равны и сами выражения:

Это утверждение можно строго доказать, например, используя свойство кубической функции (см. рис. 1).

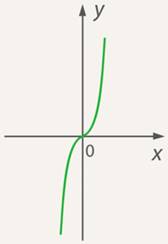
Рис. 1. График функции

Функция является монотонно возрастающей, и каждому значению соответствует ровно одно значение . Поэтому равные значения функции могут быть только при равных аргументах:

Для сравнения: функция не является монотонной (см. рис. 2).

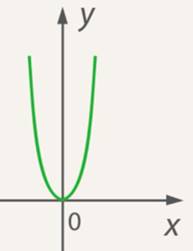
Рис. 2. График функции

Каждому положительному значению соответствуют два противоположных значения . Поэтому если значения функции равны, то аргументы или равны, или противоположны:

Так, решая уравнение , мы получаем решения:

Полученные выводы можно обобщить. Любая функция вида при нечетных будет монотонно возрастающей. Поэтому для нечетных :

А вот график функции при четных будет похож на квадратичную параболу. И каждому значению функции будет соответствовать два противоположных значения аргумента. Для четных :

Примеры решений уравнений с использованием этих свойств вы можете увидеть ниже.

 

Решение некоторых уравнений высших степеней

Пример 1. Решить уравнение:

Решение

Степени нечетные, значит, из равенства пятых степеней следует:

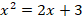
Получили квадратное уравнение:

Корни полученного уравнения можем подобрать по теореме Виета:

Подходят значения:

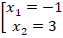
Ответ: .

 

Пример 2. Решить уравнение:

Решение

Степени четные, значит, из равенства шестых степеней следует:

Получили два линейных уравнения. Из первого:

Из второго:

Ответ:

Решение кубических уравнений

Мы знаем алгоритмы решения линейных и квадратных уравнений. Для кубических уравнений также существуют универсальные алгоритмы решения, но для них описания необходимо использовать понятие комплексных чисел (то есть расширенное множество чисел, в котором определено значение ).

Поэтому общие алгоритмы решения кубических уравнений в школьном курсе мы рассматривать не будем. Но для кубических уравнений с целыми коэффициентами, которые имеют хотя бы один целый корень, задачу можно свести к решению квадратного уравнения. Посмотрим, как это сделать.

Для начала отметим, что если некоторое число является корнем кубического уравнения 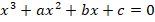, то левую часть этого уравнения можно разложить на множители:

Это аналогично тому, как многочлен можно разложить на множители:

,

где и – корни этого многочлена.

Анализируя разложение кубического многочлена, можно сделать два важных вывода, которые мы будем использовать для решения кубических уравнений:

1. Если раскрыть скобки, то свободный член . Из этого следует, что если уравнение имеет хотя бы целый корень, то его следует искать среди делителей свободного члена .

2. Чтобы найти второй множитель в разложении, необходимо разделить на :

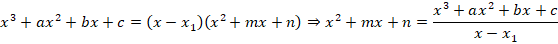
Разделить многочлены можно в столбик аналогично делению чисел в столбик. Если вы забыли, как это делать, посмотрите ниже.

 

Деление многочленов

Деление многочлена на многочлен производится по тому же принципу, что и деление чисел – столбиком (уголком). Это подбор, только подбор алгоритмизируемый. В частности, для деления многочленов нам пригодится понятие степени многочлена, которое мы вводили.

 

Пример 1. Выполнить деление:

Решение

Заметим:

Запишем в столбик:

Таким образом:

Ответ: .

Могут ли многочлены делиться друг на друга нацело? В нашем примере получилось деление с остатком:

Но бывает и так, что многочлены делятся нацело.

 

Пример 2. Выполнить деление:

Решение

Заметим, что:

Запишем в столбик:

Проверка:

Ответ: .

Задание 4. Решить уравнение:

Решение

Ищем целые корни среди делителей свободного члена (числа 3). На эту роль подходят числа . Проверяем их: если число является корнем уравнения, то при подстановке вместо переменной оно обращает уравнение в верное равенство.

При :

Равенство неверное.

При :

Равенство верное, значит, является корнем уравнения. Тогда многочлен третьей степени можно разложить на множители:

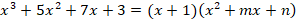
Разделим в столбик:

Получаем:

Тогда исходное уравнение примет вид:

Тогда:

Решая квадратное уравнение, получаем:

Итого, получаем всего различных корня: и .

Ответ: ; .

Аналогичным образом можно решать не только кубические уравнения, но и уравнения высших степеней. Если удастся подобрать один корень, то после деления в столбик можно понизить степень уравнения на 1. Так, как мы свели кубическое уравнение к квадратному.

Решение иррациональных уравнений

Кроме целых рациональных, мы еще сталкивались с дробно-рациональными и иррациональными уравнениями. Единственная их особенность заключается в том, что при решении нужно учитывать ОДЗ: не определено деление на ноль и извлечение квадратного корня из отрицательного числа (на множестве действительных чисел). В остальном же идея очень простая:

1. Если есть дробь, избавляемся от нее, умножая обе части равенства на соответствующие выражения.

2. Если есть корень, избавляемся от него, возводя в квадрат обе части уравнения.