ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Белгородский государственный технологический университет
Им В.Г. Шухова
Утверждено
научно-методическим советом
Университета
ЭЛЕКТРОННЫЕ ЛЕКЦИИ
ПО МАТЕМАТИКЕ ДЛЯ СТУДЕНТОВ 1-ГО КУРСА
ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ
ВСЕХ НАПРАВЛЕНИЙ
Белгород 2015
Глава 1. Матрицы и определители
Понятие матрицы
Прямоугольная таблица, состоящая из чисел, расположенных в m строках и n столбцах, называется матрицей. Матрицы обозначаются заглавными латинскими буквами, например: 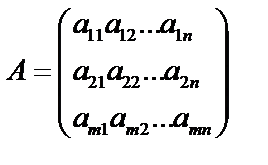 .
.
Числа m и n называются порядками матрицы. Если m = n, то матрица называется квадратной порядка n, иначе – прямоугольной. Числа 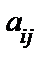 , входящие в состав матрицы, называются ее элементами, причем
, входящие в состав матрицы, называются ее элементами, причем
i – номер строки, j – номер столбца.
Строчная матрица имеет размер 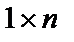 , а столбцовая матрица –
, а столбцовая матрица –  .
.
Матрица  , полученная из матрицы А заменой в ней строк на столбцы с сохранением порядка их следования, называется транспонированной. Очевидно, что
, полученная из матрицы А заменой в ней строк на столбцы с сохранением порядка их следования, называется транспонированной. Очевидно, что 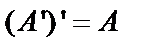 .
.
Главная диагональ квадратной матрицы – воображаемая прямая, проходящая через элементы с одинаковыми индексами из левого верхнего в правый нижний ее угол. Эти элементы – диагональные. Побочная диагональ – прямая, идущая из правого верхнего в нижний левый угол матрицы.
Квадратная матрица, у которой все элементы вне главной диагонали равны 0, называется диагональной. Среди диагональных элементов может быть и нулевые.
Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны 1, например: 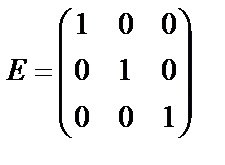 – единичная матрица третьего порядка.
– единичная матрица третьего порядка.
Основные операции над матрицами
Две матрицы называются равными, если эти матрицы имеют одинаковые порядки и все соответствующие их элементы совпадают.
Произведением матрицы А размером 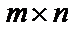 на действительное число
на действительное число  называется матрица С размером
называется матрица С размером 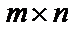 , элементы
, элементы 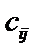 которой равны
которой равны 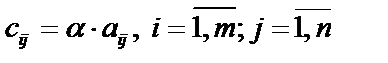 .
.
Умножение матриц на число обладает следующими свойствами:  .
.
Суммой двух матриц А и В размером 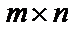 называется матрица С размером
называется матрица С размером 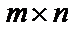 , элементы
, элементы  которой равны
которой равны  .
.
Очевидно, что сложение матриц обладает следующими свойствами:
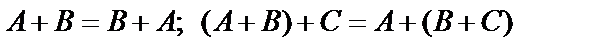 .
.
Произведением  матрицы А на
матрицы А на  матрицу В называется
матрицу В называется 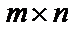 матрица С, элементы
матрица С, элементы 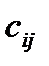 которой равны сумме произведений элементов i строки матрицы А на соответствующие элементы j столбца матрицы В:
которой равны сумме произведений элементов i строки матрицы А на соответствующие элементы j столбца матрицы В:  .
.
Произведение матриц  имеет смысл в том случае, если число столбцов матрицы А совпадает с числом строк матрицы В. В общем случае
имеет смысл в том случае, если число столбцов матрицы А совпадает с числом строк матрицы В. В общем случае 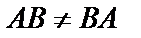 , т. е. произведение некоммутативно.
, т. е. произведение некоммутативно.
Свойства произведения матриц:
1.  (единичная матрица Е – как 1 при умножении чисел);
(единичная матрица Е – как 1 при умножении чисел);
2. 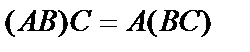 – ассоциативно;
– ассоциативно;
3.  дистрибутивный закон.
дистрибутивный закон.
Пример 1.1.  . Найти
. Найти 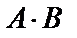 ,
, 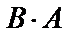 .
.

 .
.
Очевидно, что 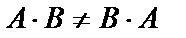 .
.
 2020-06-29
2020-06-29 94
94







