Минором любого элемента 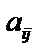 матрицы n- го порядка будем называть определитель порядка
матрицы n- го порядка будем называть определитель порядка  , соответствующий матрице, которая получена из данной вычеркиванием строчки с номером i и столбца с номером j, на пересечении которых находится данный элемент. Минор элемента
, соответствующий матрице, которая получена из данной вычеркиванием строчки с номером i и столбца с номером j, на пересечении которых находится данный элемент. Минор элемента 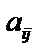 будем обозначать
будем обозначать 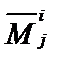 .
.
Алгебраическим дополнением  элемента
элемента 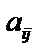 назовем число, равное
назовем число, равное 
Тогда сформулируем свойство 8 определителей:
8. Определитель равен сумме произведений элементов какой-нибудь строки (или столбца) на алгебраические дополнения этих элементов.

Последнее свойство определителей:
9. Сумма произведений элементов какой-либо строки на соответствующие алгебраические дополнения элементов другой строки равна нулю.
Ранг матрицы
Пусть имеется прямоугольная матрица размером m на n: 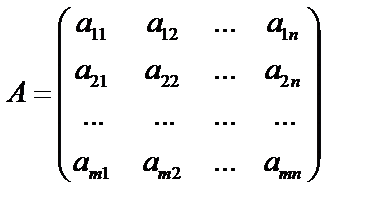 . Если в этой матрице выделить k строк и k столбцов, то мы получим квадратную матрицу порядка k. Определитель этой матрицы называется минором k – го порядка матрицы А. Среди этих миноров найдется хотя бы один, отличный от нуля, минор старшего порядка. Порядок наибольшего минора, отличного от нуля, называется рангом матрицы r(A). Тот минор r -го порядка, который отличен от нуля, назовем базисным минором (у матрицы А может быть несколько миноров r -го порядка, которые отличены от нуля). Строки и столбцы, на пересечении которых стоит базисный минор, назовем соответственно базисными строками и базисными столбцами.
. Если в этой матрице выделить k строк и k столбцов, то мы получим квадратную матрицу порядка k. Определитель этой матрицы называется минором k – го порядка матрицы А. Среди этих миноров найдется хотя бы один, отличный от нуля, минор старшего порядка. Порядок наибольшего минора, отличного от нуля, называется рангом матрицы r(A). Тот минор r -го порядка, который отличен от нуля, назовем базисным минором (у матрицы А может быть несколько миноров r -го порядка, которые отличены от нуля). Строки и столбцы, на пересечении которых стоит базисный минор, назовем соответственно базисными строками и базисными столбцами.
Свойства ранга:
1. Ранг матрицы не меняется при ее транспонировании, т.к. строки и столбцы равноправны в отношении ранга.
2. Ранг матрицы не меняется при перестановке ее строк.
3. Ранг матрицы не меняется при умножении всех элементов какой-либо строки на отличное от нуля число.
4. Ранг матрицы не меняется, если к одной из ее строк прибавить другую строку, умноженную на некоторое число.
5. Ранг матрицы не меняется, если удалить нулевую строку.
6. Ранг матрицы не меняется, если удалить строку, являющейся линейной комбинацией другой строки.
Напомним, что элементарными называются следующие преобразования матриц:
 Перестановка двух любых строк и столбцов;
Перестановка двух любых строк и столбцов;
 Умножение строки или столбца на число отличное от нуля;
Умножение строки или столбца на число отличное от нуля;
 Прибавление к одному столбцу или строке линейной комбинации других столбцов или строк.
Прибавление к одному столбцу или строке линейной комбинации других столбцов или строк.
Элементарное преобразование не меняет ранг матрицы (это следует из свойств).
Каноническойназывается матрица, у которой в начале главной диагонали стоит подряд несколько единиц, а все остальные элементы равны нулю.
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической.
Ранг канонической матрицы равен числу единиц на ее главной диагонали.
Рассмотрим другой метод вычисления ранга матрицы, называемый методом окаймляющих миноров. В рассматриваемой матрице находим элемент, отличный от нуля, тогда ранг матрицы не меньше единицы. Затем выбираем минор второго порядка (определитель), отличный от нуля и содержащий выбранный ранее элемент. Если такой минор существует, то ранг матрицы не менее двух. Далее выбираем минор 3-его порядка, отличный от нуля, в который входит минор второго порядка. Если такой минор 3-его порядка существует, то ранг матрицы не менее трех, и т.д.
Обратная матрица
Рассмотрим квадратную матрицу А порядка n: 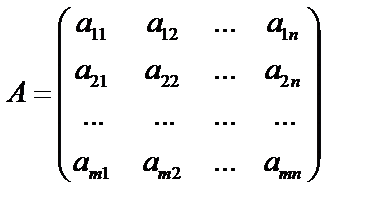 . Считаем, что матрица А – невырожденная, т.е. ее определитель отличен от нуля.
. Считаем, что матрица А – невырожденная, т.е. ее определитель отличен от нуля.
Квадратная матрица  называется обратной для матрицы А, если выполняются равенства:
называется обратной для матрицы А, если выполняются равенства:
 , где Е – единичная матрица порядка n.
, где Е – единичная матрица порядка n.
Теорема. Для того чтобы квадратная матрица А имела обратную матрицу, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
Получим формулу для обратной матрицы:  .
.
Пример 1.2. Вычислить обратную матрицу для матрицы 
Определитель матрицы  Алгебраические дополнения:
Алгебраические дополнения: 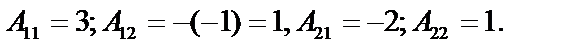
Тогда  .
.
Пример 1.3. Вычислить обратную матрицу для матрицы  .
.
1) 

2) 

 2020-06-29
2020-06-29 132
132








