2020-06-29
105
Различают скалярные и векторные величины. Скалярные величины полностью характеризуются своим численным значением в выбранной системе единиц (работа, температура, плотность и т.д.). векторы кроме численного значения, обладают направлением в пространстве. Вектором называется направленный отрезок 
с начальной точкой А и конечной точкой В. Вектор может обозначаться одной буквой: 
. Длиной (модулем) | 
| вектора 
называется число, равное длине отрезка АВ.
Векторы, лежащие на одной прямой (или на параллельных прямых) называются коллинеарными. Если начало и конец вектора совпадают, то такой вектор называют нулевым и обозначают 
. | 
| = 0, направление произвольно. Если 
= 
, то вектор 
называют противоположным к вектору 
и обозначают – 
. Очевидно, что 
.
Введем в рассмотрение прямоугольную систему координат и перенесем вектор 
параллельно самому себе так, чтобы его начало совпало с началом координат. Координатами вектора 
будем называть координаты его конечной точки: 
.
Модуль вектора 
: 
.
Линейные операции над векторами.
Пусть заданы векторы 
и 
Линейными операциями называют сложение (вычитание) векторов и умножение вектора на скаляр. Сложение векторов производят по правилу параллелограмма:
, 
. Чтобы построить сумму векторов 
, нужно к концу вектора 
приложить вектор, 
к концу вектора приложить вектор 
и так далее до 
. Тогда суммой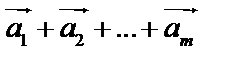 
будет вектор, идущий из начала в конец вектора .
Вычесть какой-нибудь вектор – значит прибавить противоположный, т.е. 
.
Умножение вектора 
на (скаляр) число 
: 
, 
.
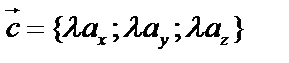Если 
, то полученный вектор – это вектор, получающийся из 
растяжением в 
раз без изменения направления. Если 
, тогда следует 
растянуть в 
раз и изменить направление на противоположное.
Свойства:
1. 
;
2. 
;
3. 
;
4. 
;
5. 
;
6. 
.
