1. Степенная. 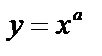 , где
, где 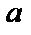 - действительное число.
- действительное число.
2. Показательная: 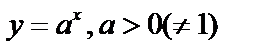 .
.
3. Логарифмическая: 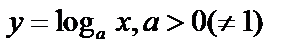 .
.
4. Тригонометрические: 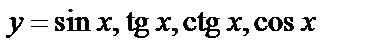 ;
;
5. Обратные тригонометрические функции: 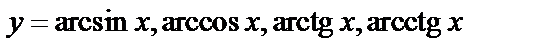 .
.
6. Сложная функция – функция вида 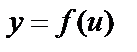 , где
, где 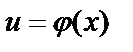 .
.
Элементарные функции. Классификация функций.
Элементарные функции – все функции, которые можно получить из основных элементарных функций с помощью:
а) алгебраических действий 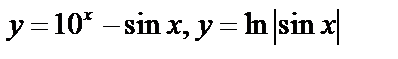 и так далее;
и так далее;
б) операцией образования сложной функции.
Неэлементарные функции: 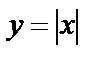 ;
; 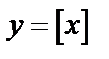 (антье) – целая часть числа х. [2,3]=2; [–2,5]=–3.
(антье) – целая часть числа х. [2,3]=2; [–2,5]=–3.
Элементарные функции можно разделить на алгебраические и трансцендентные (неалгебраические).
Алгебраической называется функция, в которой над аргументом производится конечное число алгебраических действий:
а) многочлен 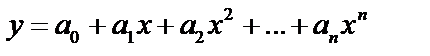 ;
;
б) дробно-рациональная функция – отношение двух многочленов;
в) иррациональная функция (если есть корни).
Всякая неалгебраическая функция называется трансцендентной. К числу трансцендентных относиться тригонометрические, показательные, логарифмические и т.д.
Глава 6. Пределы и непрерывность
6 .1. Предел числовой последовательности
Если по некоторому закону каждому натуральному числу n поставлено в соответствие вполне определенное число 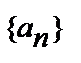 , то говорят, что задана числовая последовательность
, то говорят, что задана числовая последовательность 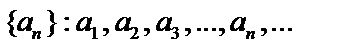 . Числа
. Числа 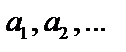 – члены последовательности,
– члены последовательности, 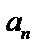 – n -й член последовательности.
– n -й член последовательности.
Число А называется пределом числовой последовательности 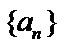 , если для любого сколь угодно малого числа
, если для любого сколь угодно малого числа 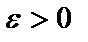 найдётся такой номер N, что для всех членов последовательности с
найдётся такой номер N, что для всех членов последовательности с 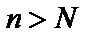 будет выполняться неравенство
будет выполняться неравенство 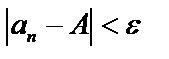 или
или 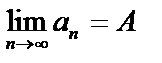 .
.
Пусть 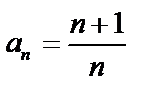 , тогда
, тогда 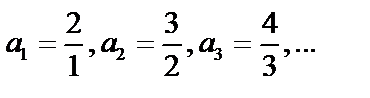 .
. 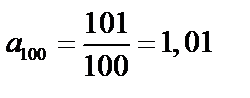
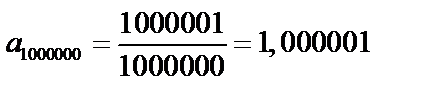 и т.д. С ростом n члены последовательности стремятся к 1, и величина разности
и т.д. С ростом n члены последовательности стремятся к 1, и величина разности 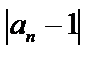 становится все меньше. Тогда
становится все меньше. Тогда 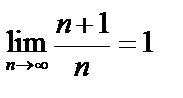 .
.
 2020-06-29
2020-06-29 119
119








