Пусть уравнение плоскости Р:  , дана
, дана  которая не принадлежит плоскости. Тогда
которая не принадлежит плоскости. Тогда  . Чтобы найти расстояние от точки до плоскости, следует подставить координаты этой точки в уравнение плоскости и полученную величину поделить на модуль вектора
. Чтобы найти расстояние от точки до плоскости, следует подставить координаты этой точки в уравнение плоскости и полученную величину поделить на модуль вектора  , т.е. на нормирующий множитель
, т.е. на нормирующий множитель  . Для определения расстояния от точки до плоскости можно пользоваться нормальным уравнением плоскости. В этом случае
. Для определения расстояния от точки до плоскости можно пользоваться нормальным уравнением плоскости. В этом случае  .
.
Уравнение плоскости, проходящей через 3 данных точки. Угол между плоскостями
Пусть точки  лежат в плоскости Р и точка
лежат в плоскости Р и точка  – любая точка плоскости. Тогда
– любая точка плоскости. Тогда  ,
,  ,
,  лежат в одной плоскости и являются компланарными. Условие компланарности: равенство нулю смешенного произведения:
лежат в одной плоскости и являются компланарными. Условие компланарности: равенство нулю смешенного произведения:  , т.е.
, т.е.
 —уравнение плоскости, проходящей через 3 точки.
—уравнение плоскости, проходящей через 3 точки.
Прямая в пространстве
В общем случае прямую в пространстве можно рассматривать как линию пересечения 2-х плоскостей: 
Канонические уравнения прямой
Пусть  – точка лежащая на прямой;
– точка лежащая на прямой;  , где m, n, p – координаты направляющего вектора прямой, т.е. вектора параллельного данной прямой.
, где m, n, p – координаты направляющего вектора прямой, т.е. вектора параллельного данной прямой.  – текущая точка.
– текущая точка.  , получаем уравнение
, получаем уравнение  – канонические уравнения прямой.
– канонические уравнения прямой.
Чтобы перейти от общего уравнения прямой к каноническому, в качестве точки  берут любое решение системы, направляющий вектор прямой можно найти как векторное произведение векторов нормалей
берут любое решение системы, направляющий вектор прямой можно найти как векторное произведение векторов нормалей 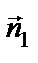 ×
×  .
.

 . Если направляющий вектор прямой задан точками M 1, M 2, то можно записать уравнение прямой, проходящей через 2 данные точки
. Если направляющий вектор прямой задан точками M 1, M 2, то можно записать уравнение прямой, проходящей через 2 данные точки  ,
,  :
:  .
.
Угол между прямыми
Пусть 2 прямые заданы в канонической форме, т.е. известны направляющие векторы каждой прямой:  ,
, 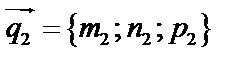 .
.
Угол  между прямыми равен углу между направляющими векторами:
между прямыми равен углу между направляющими векторами:  .
.
Если прямые параллельны, то  и
и  .
.
Если прямые перпендикулярны,  , то
, то  и
и  = 0 – условия перпендикулярности прямых.
= 0 – условия перпендикулярности прямых.
Кривые на плоскости
Окружность
Окружность- это геометрическое место точек, каждая из которых отстоит от центра (О) на одинаковом расстоянии r. Пусть  – текущая.
– текущая. 

Центр окружности:  .
.

Эллипс
Эллипс – это геометрическое место точек, для которых сумма расстояний от двух фиксированных точек, называемых фокусами, есть величина постоянная (большая расстояния между фокусами).
Пусть  , тогда
, тогда  . Вводим
. Вводим 
 ,
,
 - каноническое уравнение эллипса.
- каноническое уравнение эллипса.
Эллипс симметричен относительно осей OX и OY (x2 и y2). 
 ,
,  :
:  ;
;  ,
,  :
:  A, B, A*, B* – вершины эллипса, О – центр эллипса.
A, B, A*, B* – вершины эллипса, О – центр эллипса.  большая полуось,
большая полуось,  малая полуось.
малая полуось.
Эксцентриситет – отношение расстояния между фокусами к длине его большой оси:  ;
;  ;
;  . Для окружности a = b и ε = 0, чем больше ε, тем больше эллипс вытянут.
. Для окружности a = b и ε = 0, чем больше ε, тем больше эллипс вытянут.
Эллипс получается при сечении цилиндра и проекция окружности на плоскость.
Гипербола
Гипербола – это геометрическое место точек, для которых разность расстояний от двух фиксированных точек, называемых фокусами, есть постоянная величина, взятая по модулю и меньше расстояния между фокусами.
 и
и  - фокусы
- фокусы 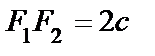 . Пусть
. Пусть  – текущая.
– текущая. 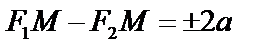
 – каноническое уравнение гиперболы.
– каноническое уравнение гиперболы.

Прямые  – асимптоты.
– асимптоты.
Эксцентриситет – отношение расстояния между фокусами гиперболы к расстоянию между ее вершинами,  , характеризует форму гиперболы.
, характеризует форму гиперболы.
Парабола
Парабола – геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки – фокуса равно расстоянию до некоторой фиксированной прямой, называемой директрисой (не проходит через фокус). Фокус F, расстояние от F до директрисы равно p – параметр параболы. Начало координат – посередине между F и директрисой.

 ,
,  ,
,  .
.
Парабола симметрична относительно ОХ. х =0, у =0. (у 2<0),  . Пусть х =1, тогда
. Пусть х =1, тогда  . Длина хорды параболы, проведенной перпендикулярно оси, равна
. Длина хорды параболы, проведенной перпендикулярно оси, равна  .
.
p характеризует «ширину» области, ограниченной параболой.
| Q |
| r |
| M |
| Y |
| d |
| p\2 |
| F (p\2,0) |
| X |
| 0 |
Глава 5. Функции
 2020-06-29
2020-06-29 138
138








