2020-06-29
90
Часто приходится рассматривать изменение одной величины в зависимости от изменения другой. При изменении движения путь рассматривается как переменная, изменяющаяся в зависимости от времени. Путь – функция времени. Если радиус круга R принимает различные значения, то площадь 
тоже будет принимать различные значения. S – функция R. Если каждому элементу x множества X ставится в соответствие определенный элемент y множества Y, то говорят, что на множестве X задана функция 
. х – независимая переменная, y —зависимая переменная.
Частные значения получаются, если аргументу х придавать частные значения. Пусть 
, 
при 
будет 
, при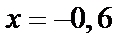 
и так далее.
Запись: 
; 
. Множество X – область определения (существования) функции, множество Y – область значений функции.
Способы задания функции
Три основных способа – аналитический, табличный, графический.
1. Аналитический способ состоит в том, что зависимость задается в виде формулы, указывающей, какие действия надо выполнить, чтобы получить значение функции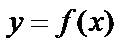 
.
2. Табличный способ заключается в том, что в определенном порядке записываются значения х и соответствующие значения у. Конечное число аргументов.
3. Графический способ часто используется в практике физических измерений. Аргументы – абсциссы, функция – ординаты. Следовательно, график 
– множество точек плоскости.
Рассмотрим основные свойства функции
1. 
–функция чётная, 
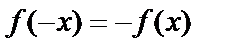– функция нечётная.
Если функция не является ни чётной, ни нечётной, то говорят, что функция общего вида.
2. Монотонность.
Функция называется возрастающей, если большему значению аргумента из множества X соответствует большее значение функции 
, то 
).
Функция убывающая, если большему значению аргумента соответствует меньшее значение функции (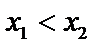
, то 
).
3. Ограниченность.
Функция 
называется ограниченной на множестве X, если существует такое положительное число 
, что 
для любого 
.
4. Периодичность.
Функция 
называется периодической с периодом 
, если выполняется равенство 
.
