Множество точек 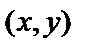 координатной плоскости ХОУ, координаты которых связаны уравнением
координатной плоскости ХОУ, координаты которых связаны уравнением 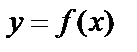 , называется графиком данной функции.
, называется графиком данной функции.
По производной функции можно судить о возрастании (убывании) самой функции. Напомним, что 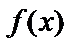 называется возрастающей в некотором интервале, если для любых
называется возрастающей в некотором интервале, если для любых 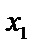 и
и  из этого интервала из неравенства
из этого интервала из неравенства 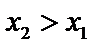 следует неравенство
следует неравенство
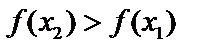 Убывающей:
Убывающей: 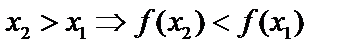 .
.
Теорема. Пусть 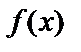 определена на отрезке
определена на отрезке 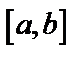 и имеет непрерывную производную
и имеет непрерывную производную 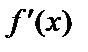 внутри отрезка. Чтобы
внутри отрезка. Чтобы 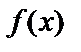 была возрастающей (убывающей), достаточно
была возрастающей (убывающей), достаточно 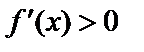 ,
, 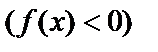 .
.
Рассмотрим возрастание. Возьмем два значения 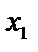 и
и 
 из
из 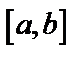 и применим формулу Лагранжа:
и применим формулу Лагранжа:  . Так как
. Так как 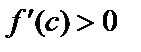 , и
, и 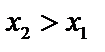 , то
, то 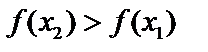 – возрастающая. Аналогично – убывающая.
– возрастающая. Аналогично – убывающая.
Геометрический смысл – производная – угловой коэффициент касательной. Значение коэффициента показывает, наклонена ли касательная вверх или вниз.
Экстремумы функции
Функция 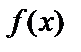 имеет в т.
имеет в т. 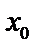 максимум, если
максимум, если  , где
, где 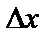 – достаточно малая по величине. Функция
– достаточно малая по величине. Функция 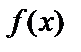 имеет в т.
имеет в т. 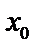 минимум, если
минимум, если 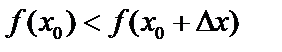 .
.
Если в т. 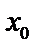
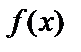 имеет max или min, то говорят, что в этой точке имеет место экстремум.
имеет max или min, то говорят, что в этой точке имеет место экстремум.
Необходимое условие экстремума. Если существует конечная производная, то по теореме Ферма 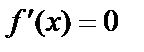 .
.
Экстремумы необходимо искать в тех точках, где 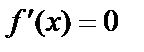 или не существует. Такие точки называются стационарными (критическими).
или не существует. Такие точки называются стационарными (критическими).
Если допустить, что в отдельных точках нет конечной производной, то следует отнести к критическим и эти точки. Критические точки следует проверить, в них необязательно экстремум (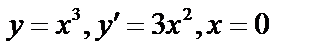 , нет экстремума).
, нет экстремума).
Первый достаточный признак экстремума.
Пусть т. 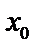 является критической для
является критической для 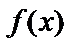 , а
, а 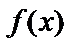 непрерывна и дифференцируема во всех точках некоторого интервала, содержащего эту точку (за исключением, возможно, самой точки
непрерывна и дифференцируема во всех точках некоторого интервала, содержащего эту точку (за исключением, возможно, самой точки 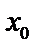 ). Тогда возможно:
). Тогда возможно:
1) 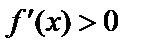 при
при 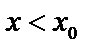 и
и 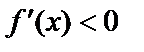 при
при 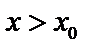 , то есть производная при переходе через т.
, то есть производная при переходе через т. 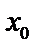 меняет знак с «+» на «–». Тогда при
меняет знак с «+» на «–». Тогда при 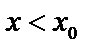
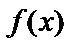 возрастает, а при
возрастает, а при 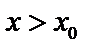 (в данном интервале) убывает, значит, значение
(в данном интервале) убывает, значит, значение 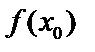 будет наибольшим – в т.
будет наибольшим – в т. 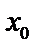
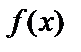 имеет max.
имеет max.
2) 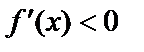 при
при 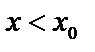 ,
, 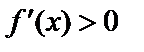 при
при 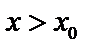 , то есть с «–» на «+» – min.
, то есть с «–» на «+» – min.
3) 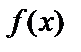 не меняет знак при переходе через
не меняет знак при переходе через 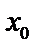 . Тогда
. Тогда 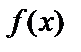 либо возрастает, либо убывает, экстремума нет.
либо возрастает, либо убывает, экстремума нет.
Второй достаточный признак экстремума.
Пусть 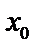 – критическая точка и
– критическая точка и 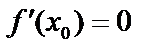 ,
, 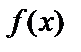 имеет вторую производную в интервале и в самой т.
имеет вторую производную в интервале и в самой т. 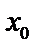 . Тогда, если
. Тогда, если 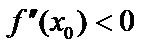 – max,
– max, 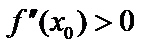 – min.
– min.
По определению производной: 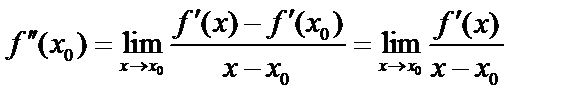 . Если
. Если  , то дробь > 0. При
, то дробь > 0. При  знаменатель <0,
знаменатель <0,  ( убывает) и при
( убывает) и при 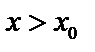 знаменатель >0 (возрастает) – min по первому признаку. Аналогично – max, если
знаменатель >0 (возрастает) – min по первому признаку. Аналогично – max, если 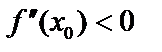 .
.
Исследования по второму признаку производят редко.
Наибольшее и наименьшее значения функции на отрезке.
Если 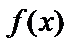 непрерывна на отрезке
непрерывна на отрезке 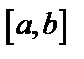 , то на этом отрезке всегда имеются точки, в которых она принимает max и min значения. Этих значений
, то на этом отрезке всегда имеются точки, в которых она принимает max и min значения. Этих значений 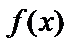 достигает или в критических точках или на концах отрезка.
достигает или в критических точках или на концах отрезка.
Правило. Чтобы определить наибольшее и наименьшее значения 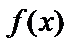 на отрезке, надо:
на отрезке, надо:
1. Определить критические точки, принадлежащие 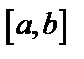 ;
;
2. Вычислить значение функции в этих критических точках и на концах отрезка;
3. Выбрать наибольшее и наименьшее значения из полученных чисел.
 2020-06-29
2020-06-29 215
215








