Определение производной. Свойства

Пусть дана функция 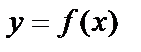, возьмем значение аргумента x и зададим ему приращение , это вызовет приращение функции .

Производная: 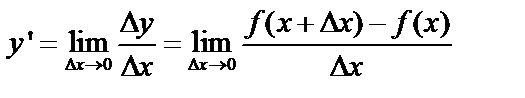, т.к. при различных значениях x производная различна,  – функция аргумента x, т.е. .

Пример. Вычислим производную . Пусть x получил приращение , тогда ; ; т.е. . 

 

Свойства производной

1) Производная , , , .

Пусть  и 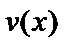 – две функции, имеющие производные.

2) ;

.

3)   

 

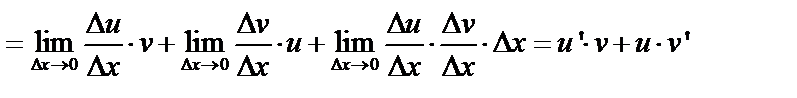, т.е.

.

4). .

5) .

 

Производная сложной и обратной функций

Сложная функция

Пусть задана функция  и функция , тогда  называется сложной функцией.

Пример. 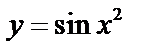; ; ; ; ;  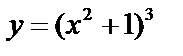и т.д.

Пусть эти функции – дифференцируемые. Пусть x получил приращение , тогда функции  и  получают приращение  и 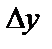. Рассмотрим . Перейдем к пределу (если , то ): .

Обратная функция

Пусть , будем считать y за аргумент, а x – за функцию. Тогда 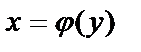 – обратная функция, может быть многозначной.

-обратная,  – двузначная функция и т.д.

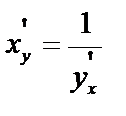Если  – монотонная функция, то существует непрерывная обратная функция . . Перейдя к пределу:  или .

Производные тригонометрических функций

а)

Воспользуемся схемой нахождения производной:

; ;

;

(учли первый замечательный предел и непрерывность функции ).

Итак, 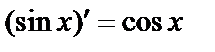 и .

б) ; ;

 и .

в) ;

;

т.е.

 и .

г) ; ;

; .

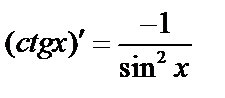Производная обратных тригонометрических функций

а) , где и .

Обратная функция имеет вид 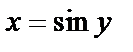, причем , если .

Используем правила дифференцирования обратной функции

.

При  производная не существует.

Итак, 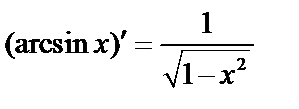 и .

б)  Поскольку , то ; .

Аналогично, ; .

; .