2020-06-29
89
Основная задача дифференциального исчисления – отыскание производной заданной функции. Однако имеется обратная задача: по данной 
найти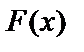 
, производная которой равна , 
.
Лемма: Функция, производная которой на некотором промежутке равна нулю, является константой.
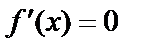по т. Лагранжа
, 
.
Теорема. Если 
– первообразная для функции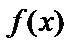 
на некотором промежутке X, то любая другая первообразная имеет вид 
.
Определение. Если функция – первообразная для 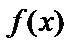, то множество функций называется неопределенным интегралом от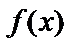 
и обозначается: 
, где 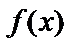– подынтегральная функция, 
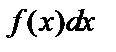– подынтегральное выражение, x – переменная интегрирования.
Восстановление функции по ее производной или отыскание неопределенного интеграла называется интегрированием.
Свойства неопределённого интеграла:
Табличные интегралы:
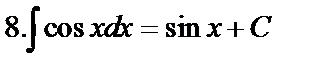
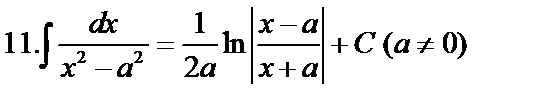
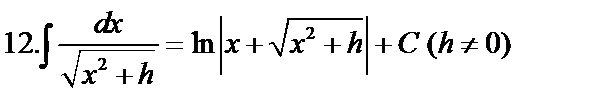
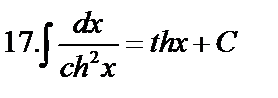
Непосредственное интегрирование
Вычисление интеграла путем использования таблиц и основных свойств называется непосредственным интегрированием.
Примеры.
.
.
Метод подстановки. Интегрирование по частям
Если известно, что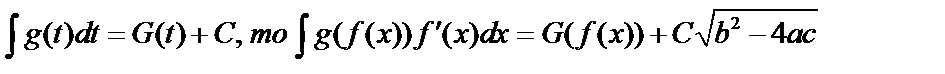 
.
Это вытекает из правила дифференцирования сложной функции.
Примеры:
.
.
.
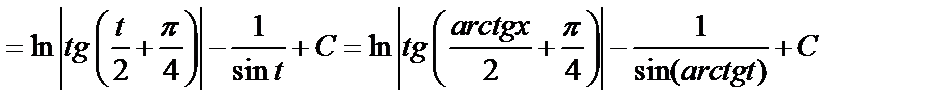Интегрирование по частям
Нет формулы, выражающий интеграл от произведения функций через интеграл от сомножителей. Интеграл от элементарной функции не всегда является элементарной функцией.
Пусть имеются дифференцируемые функци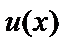и 
и 
: 
или, интегрируя, получим: 
– формула интегрирования по частям.
При использовании формулы интегрирования по частям необходимо выбрать функцию, тогда оставшаяся часть будет дифференциалом функции 
, т.е. 
. Можно указать следующие случаи:
1. 
.
В этом случае последовательное дифференцирование уменьшает показатель 
до нуля. Наиболее простой случай, когда 
.
2. 
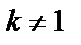
В этом случае дифференцирование указанных функций обычно упрощает нахождение интеграла.
Примеры:
1) 
2.) 
3.) 
4.) 
, тогда
.
