2020-06-29
107
Рассмотрим рациональную функцию вида 
, где 
и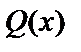 
– многочлены. Многочлен – это выражение вида 
.
Если степень многочлена в числителе равна или больше степени многочлена в знаменателе, то дробь называется неправильной и необходимо выполнить деление:
, где 
– многочлен.
Пример
а) 
.
б)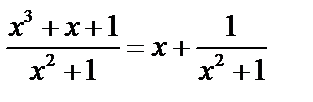 
.
Далее будем рассматривать правильные дроби (т.е. старшая степень числителя меньше старшей степени знаменателя), т. к. интегрирование функции 
– табличное. Если 
– корни уравнения 
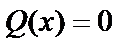, то многочлен можно представить в виде 
, где 
– коэффициент при старшей степени многочлена. Выражения 
называют линейным множителем.
Среди корней могут быть и комплексные, в этом случае элементарными множителями будут выражения 
. Кроме того, корни могут быть кратными (одинаковыми). Окончательно имеем: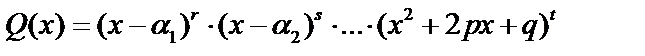 
где 
.
В высшей алгебре доказывается, что правильную дробь можно представить в виде простейших дробей: 
Это разложение рациональной функции на простейшие дроби.
10.4. Интегрирование простейших дробей
Чтобы определить числа 
, умножим обе части разложения на 
и приравняем коэффициенты при одинаковых степенях x в левой и правой части равенства.
|
|
|
Пример: 
;
Алгоритм.
1.Выделить правильную дробь.
2.Знаменатель разложить на элементарные множители.
3.Найти коэффициенты в разложении 
на простейшие дроби.
После этого задача сводится к нахождению интегралов 4 типов:
. 
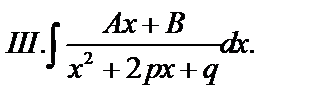
Вычислим интеграл типа III.
Выделим в знаменателе полный квадрат:
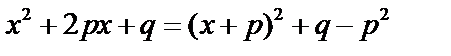. Используем подстановку, 
.
.
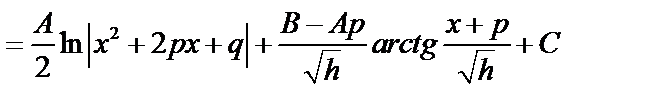Пример:
.
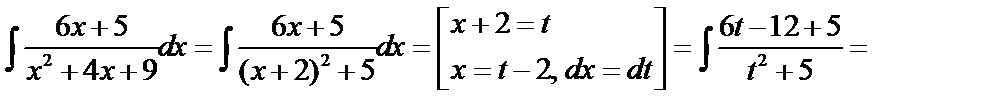
Вычисление интеграла типа IV.
В числителе записывается производная знаменателя: 
и
, где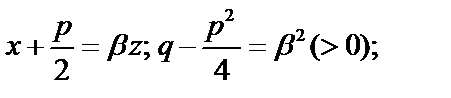 
.
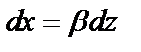Интегралы вида 
вычисляются по рекуррентной формуле:
(или формула приведения). Зная, что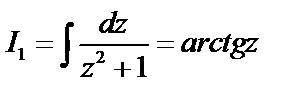 
можно вычислить 
Пример.
; по формуле приведения: 
, окончательно,
