Пусть функция 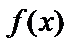 определена и непрерывна при всех
определена и непрерывна при всех  .
.
Тогда несобственный интеграл  . Если предел существует, то интеграл существует или сходится, если предел не существует, то интеграл расходится (не существует), т.е. не имеет конечного значения.
. Если предел существует, то интеграл существует или сходится, если предел не существует, то интеграл расходится (не существует), т.е. не имеет конечного значения.
Геометрический смысл:  выражает площадь бесконечной области, заключенной между линиями
выражает площадь бесконечной области, заключенной между линиями  .
.
Аналогично,  .
.
Для последнего равенства должны существовать оба интеграла, с – число.
Пример 1. Исследовать на сходимость несобственный интеграл: 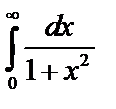 .
.
y
0 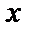
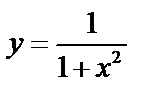
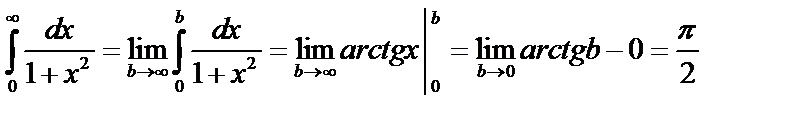 .
.
Пример 2. При каких значениях параметра α интеграл  сходится и при каких расходится?
сходится и при каких расходится?
 .
.

Пример 3. 
 .
.
Если требуется установить, сходится ли данный интеграл или расходится, удобно применять теоремы:
1. Если для всех 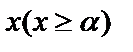 выполняется неравенство
выполняется неравенство  и если
и если  сходится, то
сходится, то  тоже сходится и
тоже сходится и 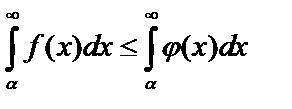 .
.
2. Если для всех 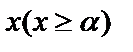 :
:  причем
причем  расходится, то и
расходится, то и  расходится.
расходится.
3. Если  сходится, то и
сходится, то и  сходится.
сходится.
Пример 4. Сходится ли 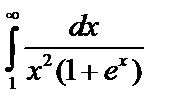 ?
?
При 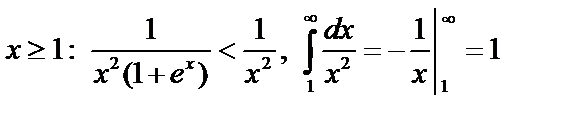 , поэтому (т.1)
, поэтому (т.1)  тоже сходится и < 1.
тоже сходится и < 1.
Пример 5. Исследовать  .
.
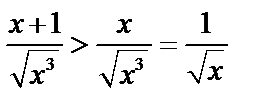 . Но
. Но 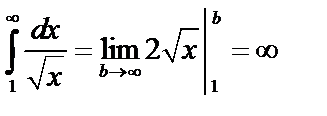 – расходится, поэтому рассматриваемый интеграл тоже расходится.
– расходится, поэтому рассматриваемый интеграл тоже расходится.
Пример 6. Исследовать 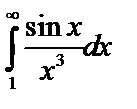 на сходимость.
на сходимость.
Подынтегральная функция знакопеременная.  Но
Но 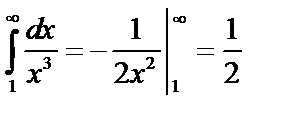 , значит, интеграл
, значит, интеграл  сходится, и по т.3 сходится и
сходится, и по т.3 сходится и 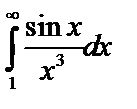 .
.
Несобственные интегралы от функций, имеющих разрыв
Пусть функция  определена и непрерывна при
определена и непрерывна при  , а при
, а при 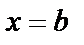 функция либо не определена, либо терпит разрыв. В этом случае нельзя говорить об
функция либо не определена, либо терпит разрыв. В этом случае нельзя говорить об 
 , как о пределе интегральной суммы, поскольку этот предел может не существовать.
, как о пределе интегральной суммы, поскольку этот предел может не существовать.
Интеграл  Если предел существует, то интеграл сходится, иначе – расходится.
Если предел существует, то интеграл сходится, иначе – расходится.
Если функция имеет разрыв при  , то
, то  – аналогично, если предел существует, то интеграл сходится, иначе – расходится.
– аналогично, если предел существует, то интеграл сходится, иначе – расходится.
Если  имеет разрыв в точке
имеет разрыв в точке  внутри отрезка
внутри отрезка 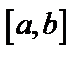 , то
, то  – существует, если существуют оба интеграла в правой части.
– существует, если существуют оба интеграла в правой части.
Пример 1. Исследовать сходимость  .
.
 – сходится.
– сходится.
Пример 2. 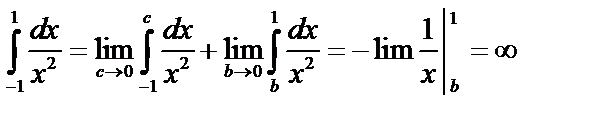 – интеграл расходится.
– интеграл расходится.
Геометрические приложения определенного интеграла
 2020-06-29
2020-06-29 91
91








