Пусть 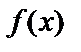 – непрерывная на отрезке
– непрерывная на отрезке 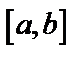 неотрицательная функция.
неотрицательная функция.
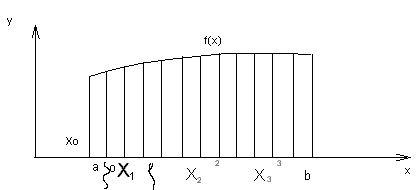
Определим площадь криволинейной трапеции – фигуры, ограниченной прямыми 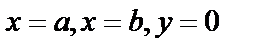 и графиком функции
и графиком функции 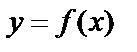
Разобьем 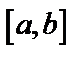 на n частей точками
на n частей точками 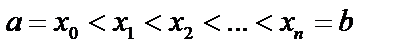 , выберем на каждом из частичных отрезков
, выберем на каждом из частичных отрезков 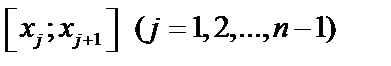 по произвольной точке
по произвольной точке 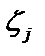 определим значение функции
определим значение функции 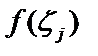 (в этих точках) и составим сумму:
(в этих точках) и составим сумму:  .
.
Эта сумма равна сумме площадей 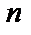 прямоугольников. Устремим
прямоугольников. Устремим 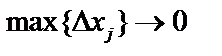 Если при этом
Если при этом 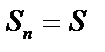 , и
, и 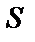 не зависит от способа разбиения и выбора точек
не зависит от способа разбиения и выбора точек 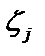 , то величина
, то величина 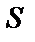 называется площадью данной криволинейной трапеции:
называется площадью данной криволинейной трапеции:  .
.
Каждая криволинейная трапеция, соответствующая непрерывной функции 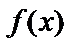 , имеет площадь
, имеет площадь 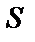 .
.
Указанный предел называется определённым интегралом и обозначается:  .
.
Числа 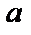 и
и 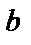 называются нижним
называются нижним 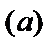 и верхним
и верхним 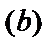 пределами интегрирования,
пределами интегрирования, 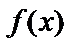 – подынтегральная функция,
– подынтегральная функция,  – переменная интегрирования.
– переменная интегрирования.
Определенный интеграл – это число.
Вычисление определённого интеграла по определению можно осуществить с помощью компьютера, однако на практике используют формулу Ньютона – Лейбница.
Пусть задана непрерывная на 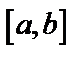 функция
функция 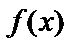 и пусть
и пусть 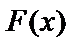 – ее первообразная. Тогда
– ее первообразная. Тогда 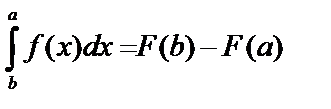 или
или 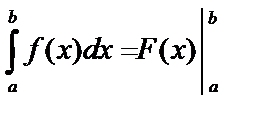 – определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего и нижнего пределов.
– определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего и нижнего пределов.
Определенный интеграл с переменным верхним пределом: 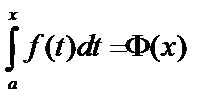 – функция
– функция 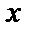 .
.
Если 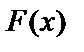 – первообразная для
– первообразная для 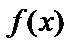 , то
, то 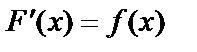 и по формуле Ньютона – Лейбница:
и по формуле Ньютона – Лейбница: 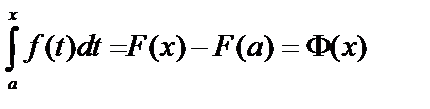 . Дифференцируем:
. Дифференцируем: 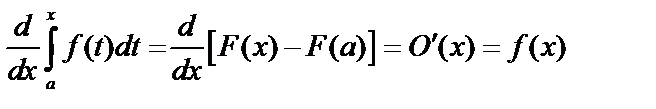 – производная по верхнему пределу равна подынтегральной функции.
– производная по верхнему пределу равна подынтегральной функции.
Свойства определённого интеграла
1.  – не зависит от значения переменной интегрирования.
– не зависит от значения переменной интегрирования.
2. 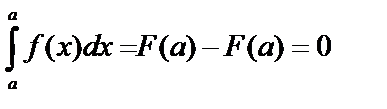 .
.
3. 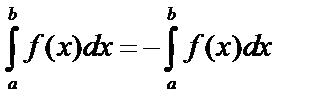 .
.
4.Для любых чисел a, b, c: 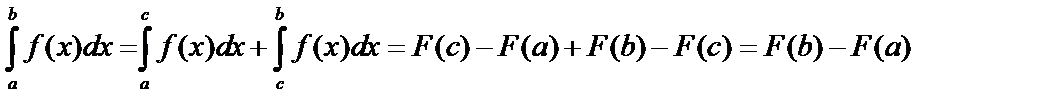 .
.
5. 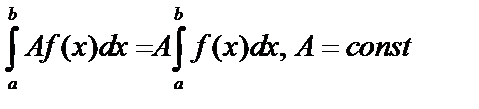 .
.
6. 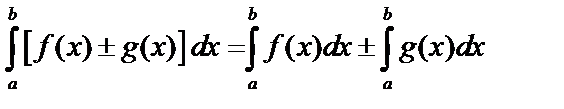 .
.
7. Если 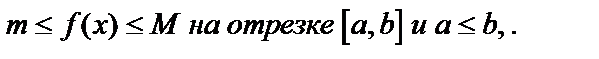
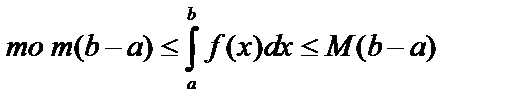
8.  – теорема о среднем.
– теорема о среднем.
Пример: 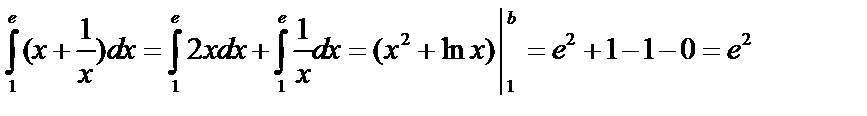 .
.
Интегрирование по частям и замена переменной в определенном интеграле
Пусть 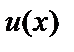 и
и 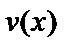 – две непрерывные дифференцируемые функции на отрезке
– две непрерывные дифференцируемые функции на отрезке  , тогда
, тогда
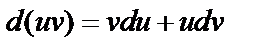 . Проинтегрируем равенство от a до b:
. Проинтегрируем равенство от a до b:
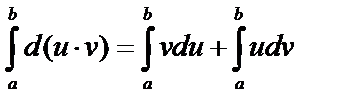 , имеем:
, имеем: 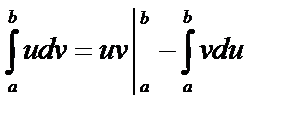 – формула интегрирования по частям.
– формула интегрирования по частям.
Пример. 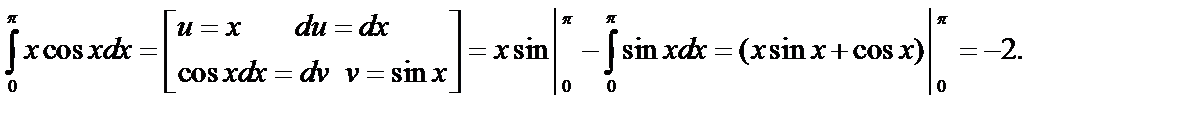
Замена переменнойвопределённом интеграле
Пусть дан интеграл 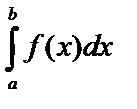 , где
, где  непрерывная функция на
непрерывная функция на 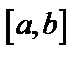 . Введем новую переменную по формуле
. Введем новую переменную по формуле 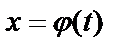 . Если
. Если 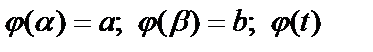 и
и 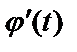 непрерывны на
непрерывны на 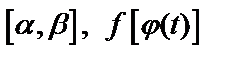 непрерывна на
непрерывна на 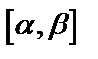 , то:
, то: 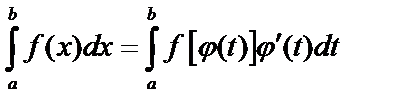 .
.
 2020-06-29
2020-06-29 114
114








