Интегрирование тригонометрических функций

Интеграл вида , где – рациональная функция от 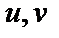 всегда выражается через элементарные функции.

1) Часто используется универсальная подстановка:

 

,

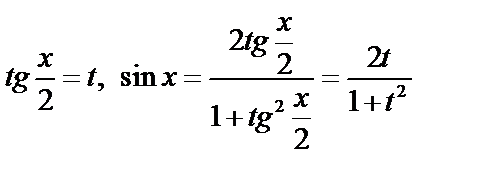и получается  от рациональной функции .

Использование этой подстановки обычно связано с громоздкими вычислениями.

2) Если имеет место тождество , то можно применить подстановку .

Пример 1.  

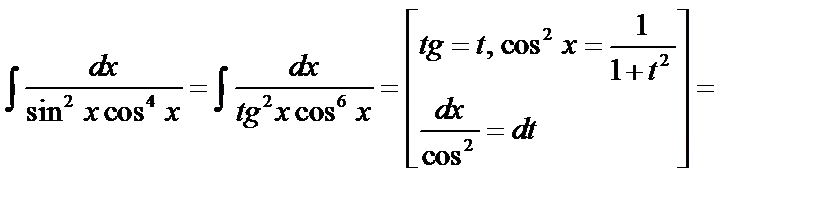
Пример 2.

.

3) Интегралы вида , где m и n – целые числа любого знака.

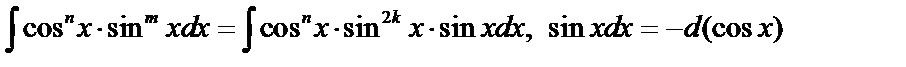а) если  – нечетное, тогда  , используется подстановка. .

б) если n – нечетное, тогда .

в) если m и n четные, то можно использовать подстановку , или понизить степень:

.

4) Часто используют формулы:

 

,

,

.

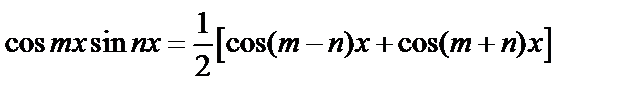Пример3.

.

 

Интегрирование некоторых иррациональных функций

I. Рассмотрим интеграл вида 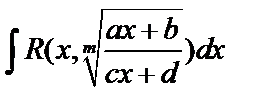, где  – рациональная функция. Используем подстановку  тогда необходимо вычислить , т.е. интеграл от рациональной функции. Затем возвращаемся к переменной . По этой же методике можно вычислять и . Необходимо привести к общему знаменателю  и : если он равен , то положить .

Пример 1.

.

.

 

Пример 2.

.

II. Интегралы вида  - подстановка .

Пример 3.

.

.

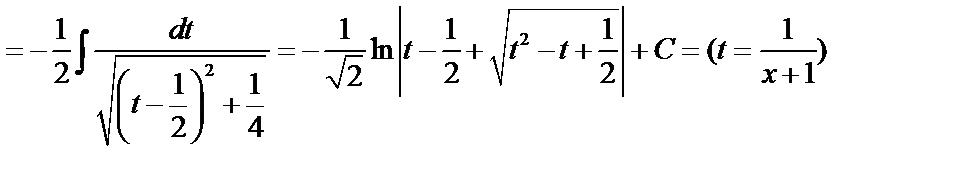III. Тригонометрические подстановки:

а) Если интеграл содержит радикал , то подстановка .

б) Если интеграл содержит радикал , то подстановка .

в) Если интеграл содержит радикал , то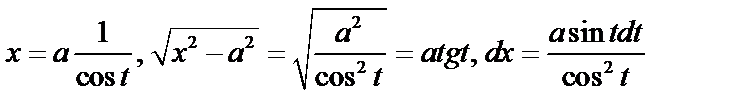  

IV. .

Например: .

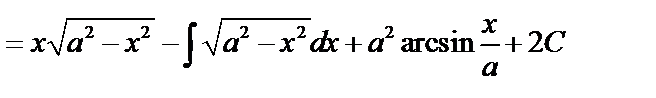тогда

. Аналогично для второго интеграла.

 

Глава 11. Определенный интеграл