2020-06-29
669
Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:
F (t) = ma (t) = –m ω^2 x X(t)
В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:
Fупр = –kX.
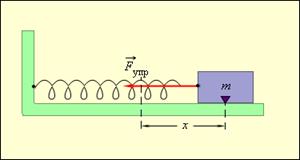
Yравнение колебаний пружинного маятника имеет вид линейного дифференциального уравнения второй степени:
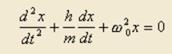
Решение этого уравнения имеет вид затухающих колебаний:
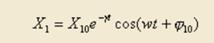
где X10, 10 — начальные амплитуда и фаза колебаний, w — частота затухающих колебаний, — декремент затухания. Подставим, получим
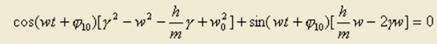
Логарифмическим декрементом затухания λ называется натуральный логарифм отношения двух последовательных амплитуд, взятых через период. Логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз.
|
|
|
Если χ = 0,01, то N = 100.
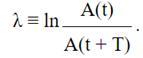
Подставим в формулу A(t) = A0 e−βt , Формула выражает связь между логарифмическим декрементом затухания и коэффициентом затухания β.
