Поиск решений в пространстве целей

 

Цель редуцируется до тех пор, пока не получим решение тривиальной задачи. Поиск решений в пространстве целей отображается деревом целей.

 

 

Существует два типа вершин: вершина И, вершина ИЛИ.

Корень дерева – главная цель.

Вершина типа И: чтобьы решить задачу, надо решить все её подзадачи.

Вершина типа ИЛИ: чтобьы решить задачу, надо решить одну из её подзадач.

 

       Вершина разрешима, если существует путь, связывающий целевую вершину с подзадачами.

       Решающий подграф – это подграф исходного графа, показывающий, что начальная вершина разрешима.

       Если в дереве есть вершины типа ИЛИ, то решающий подграф может быть не единственным.

       Просмотр вершин от листьев к корню даёт план решения задачи.

           

       В пример это могут быть: Z3 Z4 Z5

                                                       Z1 Z2

                                           Или Z3 Z4 Z6

 

       Одним из универсальных методов редукции является метод уменьшения различий. (Generel Problem Solver. Nowell, Show, Simon).

       В этом методе редукция ведётся по принципу отщепления от главной задачи элементарных подзадач.

       Sн => Sк

       Три шага:

1. Задача: преобразовать sн Sн в sк Sк, уменьшить различие.

Если D(sн,Sн)=0, то задача решениа.

2. Найти преобразование p_i P, устраняющее D(sн,Sн).

Sк = s' Spi

Если sн Sp_i, то останов.

3. Применить p_i.     

 

 

 

                                                                               p_i

	Sн => Spi		s’ Spi => Sк

 

Выводы:

1) Может существовать неединственный оператор, устраняющий различия.

2) Ветвь может оказаться тупиковой.

 

Если различия можно упорядочить по важности, то строится следующая матрица.

Dj \ Pj	P1	P2	…	Pn
V
K

 

В первую очередь применяются операторы, устраняющие главное различие.

Эффективность данного метода низкая.

 

Пример:

Обезьяна и банан.

s = (w, x, y,z)

О – обезьяна, Б – банан, Я – ящик. Система координат одномерная.

w – координата О.

y – координата ящика.

x = 1, если О на Я

       0, иначе.

z = 1, если О схватила Б

       0, иначе.

s_н = (a, 0, b, 0)

s_к = (c, 1, c, 1)

 

Операторы (преобразования):

P1(v) подойти в точку v.

P1(v) = ((x, 0, y, z) 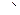 (v, 0, y, z)

P2(t) передвинуть ящик в точку t.

P2(t) = ((x, 0, x, z) 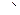 (t, 0, t, z))

P3   взобраться на ящик.

P3   = ((x, 0, x, z) 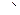 (x, 1, x, z))

P4   схватить банан.

P4   = ((c, 1, c, 0) 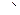 (c, 1, c, 1))

 

 

(a, 0, b, 0) (c, 1, c, 1)

Главное различие

s’ Sp4 (c, 1, c, 1)

(a, 0, b, 0) Sp4

z 1

 

                                                                               p₄

 

 

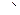Различия: D(a, 0, b, 0) Sp₄

1) Я не в точке с 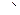P2(c)

2) О не в точке с 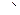P1(c)

3) О не на Я 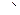P3

 

P2(c)           P1(c)                 P3

 

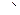                               Различия: D(c, 0, c, 0) Sp₄

                               О не на Я 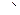P3

           P1(b)

Элементарная подзадача

 

                      P3

 

Обход снизу даёт решение: P1(b), P2(c), P3, P4.