Критерии оценки эффективности эвристических алгоритмов

1) Критерий направленности. P

   L – длина найденного пути в числе раскрываемых вершин.

                   T – общее число раскрываемых вершин.

                   P = 1 => минимальное число вершин.

                  

2) Критерий эффективности ветвлений. B

                

3) Оценка качества приближённого решения. K

             

K = 0 => оптимальное решение.

 

 

Базовые эвристики сокращения поискового пространства.

 

1) Перебор этапами (метод maxmin).

2) Ограничение числа дочерних вершин (a-b отсечение)

3) Упорядочение преобразований P_i ()

 

Пример:

Полный перебор _   _ f(s) = f1(s) + W(s) _   _ f(s) = f1(s) + (P(s) + 3Q(s)) P 0.108 0.385 0.419 B 1.86 1.31 1.08

 

 

       P(s) – сумма расстояний каждой фишки от своего места.

       Q(s) – Если фишка нецентральная, то за неё даётся 2 очка, когда за ней следует целевая (фишка на своём месте);

Если фишка центральная, то за неё даётся 1 очка, когда за ней следует целевая (фишка на своём месте);

 

Задача эвристического поиска

Задача эвристического поиска

       , где

S – множество состояний;

- множество допустимых состояний;

- множество начальных состояний; 

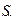- множество конечных состояний;

- множество преобразований.

 

Правила преобразований (P: S®S) могут быть заданы в виде продукционных правил:

           

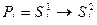
Пусть на вход поступает . Возможны следующие ситуации:

1). P не применимо к  (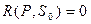). Возможны два случая:

   a). Нет применимых правил (база правил P не полна).

   b). Процесс поиска бесконечен.

2). P применимо к  (). Возможны два случая:

    a). Результат конечен:

               - единственный;

               - неединственный (можно говорить о поиске оптимального (наилучшего)

                  решения относительно критерия Q).

    b). Результат бесконечен.

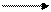
                                  Допускается бесконечное ветвление, при том условии, что

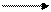
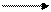
                         если был выбран какой-то путь, то до конца добираемся

                                  за конечное число шагов.

Типы задач

1. Задача планирования.

известны: 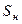 и .

найти: последовательность преобразований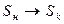

2. Задача прогнозирования.

  известно: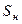

найти:     

3. Задача диагностики.

известно:

найти: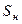   

 

Поиск в системе продукций

PS=< БП(БЗ), РП(БД),I >, где

БП – база правил

РП – рабочая память (база данных)

I - интерпретатор, реализующий стратегии поиска.

 

Продукционный цикл

1 этап.   Сопоставление и множества продукций из P.

Получаем конфликтное множество 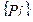CS=  ; CS 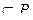 - множество тех правил, левые части которых сопоставимы с .

2 этап.   Разрешение конфликтов.

Выбирается процедура(стратегия) разрешения конфликта. В результате получаем

AS= ; AS  - активное множество.

3 этап.   Выполнение правил из AS.

В результате получаем множество . Если , то STOP. Иначе – goto 1.()

 

                                           Реализация выбора правил