Поиск решения в пространстве состояний на основе эвристической функции

Задача эвристического поиска

       , где

S – множество состояний;

- множество допустимых состояний;

- множество начальных состояний; 

- множество конечных состояний;

- множество преобразований.

Задача: нахождение последовательности преобразований :

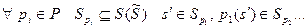
                             Система поиска

                                                                                                   

Недетерминированный выбор

                                                                                           

Реализация

Оценка альтернатив и выбор альтернативы

                                                              

 

                                                                                                                        

                                                                                                                                          +

 

 

U-ветвление. Вводится предикат P, определенный на множестве , который имеет значение истина, если это ветвление может быть применено.

U- ветвление корректно Û

Способы сокращения поискового пространства

1). Укрупнение пространства поиска. Переход от элементарных состояний к

макросостояниям.

                              

                                                               

                                                    

Проблема поиска решается в укрупненном пространстве.

2). Использрвание эвристик.

3). Изменение представления задачи.

 

Пример

Вопрос: сколько ходов нужно сделать, чтобы поменять коней местами.

1	2	3
4	5	6
7	8	9

 

 

Ответ: 16 ходов (4 – если разрешить им передвигаться ||)

Поиск решения на основе эвристической функции.

 

       Допустимый алгоритм – это тот алгоритм, который гарантирует отыскание решения.

       Оптимальный алгоритм – это допустимый алгоритм, который находит решение за минимальное число шагов.

 

       f(s) = f₁(s) + f₂(s) -> min

 

f₁(s) – оценка пройденного пути.

f₂(s) – оценка оставшегося пути.

_   _    _

f(s) = f₁(s) + f₂(s) -> min

 

_         _ f2(s)  f2(s)

       Теорема.

_         _ f2 А1(s)  f2 А2(s)

       Чтобы алгоритм, построенный на основе эвристической функций f был допустим, необходимо и достаточно, что                 .

 

       Алгоритм А1 более информирован, чем А2 ó

 

 

Критерий эффективности алгоритма поиска.

1) Стоимость решающего пути. S -> min. (допустимый алгоритм)

2)

_ f2(s)

Количество раскрываемых при поиске вершин. (оптимальный алгоритм)

3) Объём вычислений, требуемых для получения оценки       V -> min.

4) Интегральная оценочная функция.

a₁S + a₂N + a₃V -> min