1. Равномерным называется распределение вероятностей непрерывной случайной величины X, плотность которого имеет вид
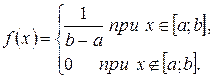
Это значит, что f(x) сохраняет постоянное значение на [ a; b ].
Функция распределения равномерного закона
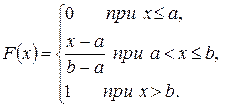
Вероятность попадания в интервал (x1; x2) непрерывной случайной равномерно распределенной величины X
P(x1<X<x2) = 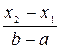 .
.
Математическое ожидание, дисперсия и среднее квадратическое отклонение равномерного распределения:

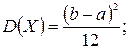

2. Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X, которое описывается плотностью
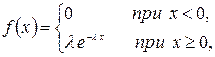
где l - постоянная положительная величина.
Функция распределения показательного закона
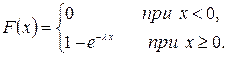
Вероятность попадания в интервал (a, b) непрерывной случайной величины X, распределенной по показательному закону,
P(a<X<b) = 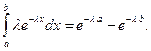
Математическое ожидание, дисперсия и среднее квадратическое отклонение показательного распределения:
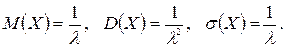
Пример 19. (Варианты 2,3)
Цена деления прибора равна 0,1. Показания прибора округляются до ближайшего целого. Найти: а) вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02; б) M(X), D(X), s(X), если случайная величина X – ошибка округления.
Решение: Ошибку округления рассматриваем как случайную величину X, равномерно распределенную между двумя соседними целыми делениями.
Тогда плотность распределения 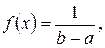 где b-a – длина интервала распределения значений X; вне этого интервала f(x)=0.
где b-a – длина интервала распределения значений X; вне этого интервала f(x)=0.
b-a =0,1 (цена деления прибора), поэтому 
Ошибка отсчета превысит 0,02, если X попадает в интервал (0,02;0,08).
P(x1<X<x2) = 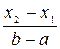 или P(x1<X<x2) =
или P(x1<X<x2) = 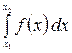 .
.
P (0,02< X <0,08)= 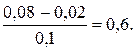
Математическое ожидание X (считаем a =0, b =0,1)
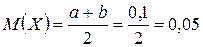 .
.
Дисперсия 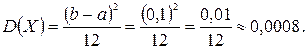
Среднее квадратическое отклонение 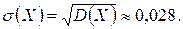
Пример 20. (Варианты 1,4,5,6)
Автобусы идут строго по расписанию. Интервал движения 7 минут. Найти: а) вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее двух минут; б) вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус не менее трех минут; в) математическое ожидание и среднее квадратическое отклонение случайной величины X – времени ожидания пассажира.
Решение: Время ожидания пассажирарассматриваем как случайную величину X, равномерно распределенную между приходами двух автобусов.
По условию задачи длина интервала распределения значений X b-a =7,
здесь b=7, a =0.
а) Время ожидания будет менее двух минут, если X попадает в интервал (5;7).
P(x1<X<x2) = 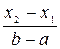 ; P (5< X <7)=
; P (5< X <7)= 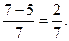
б) Время ожидания будет не менее трех минут, если X попадает в интервал (0;4).
P (0< X <4)= 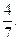
в) Математическое ожидание  .
.
Среднее квадратическое отклонение 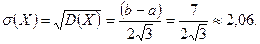
Пример 21. (Варианты 7, 8, 9, 10)
Показательное распределение задано при 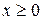 плотностью f(x)=5e -5x. Требуется: а) записать выражение для функции распределения; б) найти вероятность того, что в результате испытания X попадает в интервал (1, 4); в) найти вероятность того, что в результате испытания
плотностью f(x)=5e -5x. Требуется: а) записать выражение для функции распределения; б) найти вероятность того, что в результате испытания X попадает в интервал (1, 4); в) найти вероятность того, что в результате испытания 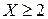 ; г) вычислить M(X), D(X), s(X).
; г) вычислить M(X), D(X), s(X).
Решение:
В данной задаче l=5
а) 
б) 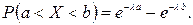
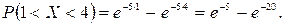
в) 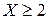 , значит a =2, b =
, значит a =2, b =  , т. е.
, т. е.
 (т.к.
(т.к. 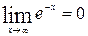 )
)
г) для показательного распределения
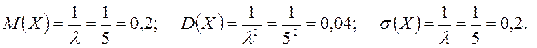
 2020-06-29
2020-06-29 121
121








