Дискретной называют случайную величину, возможные значения которой есть отдельные изолированные числа, которые эта величина принимает с определенными ненулевыми вероятностями. Число возможных значений может быть конечным или бесконечным (счетным).
Законом распределения дискретной случайной величины называют перечень её возможных значений и соответствующих им вероятностей. Закон распределения может быть задан одним из следующих способов.
1. Таблицей
| х | х1 | х2 | … | хn |
| р | р1 | р2 | … | pn |
где  .
.
2. Аналитически  . Например:
. Например:
а) биномиальное распределение
 , 0<р<1, k=0, 1, 2, …, n;
, 0<р<1, k=0, 1, 2, …, n;
б) распределение Пуассона
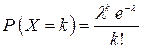 , l>0, k=0, 1, 2, ….
, l>0, k=0, 1, 2, ….
3. С помощью функции распределения F(x), определяющей для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x, т. е. 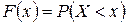 .
.
Свойства F(x):
1) 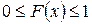 ;
;
2) 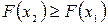 , если
, если  ;
;
3) 
4. Закон распределения может быть задан графически - многоугольником распределения (см. пример 11).
Числовые характеристики дискретных случайных величин
Математическое ожидание 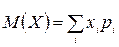 ;
;
Дисперсия  или
или  ;
;
Среднее квадратическое отклонение s(X) = 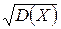 .
.
Для биномиального распределения М(X)=np, D(X)=npq. Для распределения Пуассона М(X)=l, D(X)= l.
Пример 11. (Варианты 1,5)
Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте, построить многоугольник распределения. Найти функцию распределения F(x) и построить её график. Найти М(X), D(X), s(X).
Решение: Дискретная случайная величина Х (число отказавших элементов в одном опыте) имеет следующие возможные значения: х1=0 (ни один из элементов устройства не отказал), х2=1 (отказал один элемент), х3=2 (отказало два элемента) и х4=3 (отказали три элемента).
Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что, по условию, n=3, р=0,1 (следовательно, q=1–0,1=0,9), получим: Р3(0)=q3=0,93=0,729; 
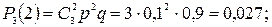

Контроль: 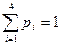 ; 0,729+0,243+0,027+0,001=1.
; 0,729+0,243+0,027+0,001=1.
Искомый биномиальный закон распределения Х: 
| Х | 0 | 1 | 2 | 3 |
| р | 0,729 | 
| 
| 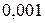
|
Для построения многоугольника распределения строим прямоугольную систему координат. По оси абсцисс откладываем возможные значения хi, а по оси ординат – соответствующие им вероятности рi. Построим точки М1 (0;0,729), М2 (1;0,243), М3 (2;0,027), М4 (3;0,001). Соединив эти точки отрезками прямых, получаем искомый многоугольник распределения (Рис.1).

Рис.1
Найдем функцию распределения F(x)=Р(Х<х).
Для  имеем F(x) = Р(Х<0)=0;
имеем F(x) = Р(Х<0)=0;
для  имеем F(x) = Р(Х<1)=Р(Х=0) =0,729;
имеем F(x) = Р(Х<1)=Р(Х=0) =0,729;
для  F(x) = Р(Х <2)= Р(Х =0)+ Р(Х =1)=0,729+0,243=0,972;
F(x) = Р(Х <2)= Р(Х =0)+ Р(Х =1)=0,729+0,243=0,972;
для  F(x)=Р(Х <3)= Р(Х =0)+ Р(Х =1)+ Р(Х =2)=0,972+0,027=0,999;
F(x)=Р(Х <3)= Р(Х =0)+ Р(Х =1)+ Р(Х =2)=0,972+0,027=0,999;
для х >3 будет F(x) =1, т. к. событие достоверно.
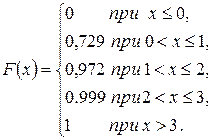 .
.
График этой функции приведен на Рис. 2.
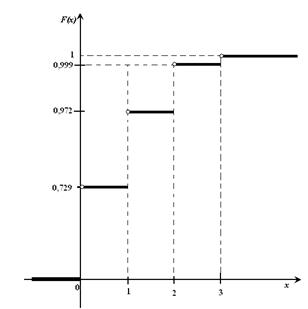
Рис. 2
Для биномиального распределения М(X)=np =3×0,1=0,3; D(X)=npq =3×0,1×0,9=0,27; s(X)=  .
.
Пример 12. (Вариант 2)*
В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Составить закон распределения случайной величины X – числа стандартных деталей среди отобранных. Найти М(X), D(X).
Решение: Случайная величина Х – число стандартных деталей среди отобранных деталей – имеет следующие возможные значения: х1 =0; х2 =1; х3 =2. Найдем вероятности возможных значений Х по формуле (пример 2)  (N – число деталей в партии, n – число стандартных деталей в партии, m – число отобранных деталей, k – число стандартных деталей среди отобранных), находим:
(N – число деталей в партии, n – число стандартных деталей в партии, m – число отобранных деталей, k – число стандартных деталей среди отобранных), находим: 


Составим искомый закон распределения:
| Х | 0 | 1 | 2 |
| р | 
| 
| 
|
Контроль:  +
+  +
+  =1.
=1.
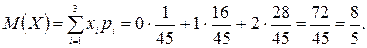
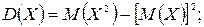

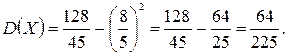
Пример 13. (Варианты 3,4)*
В устройстве независимо друг от друга выходят из строя три элемента. Вероятность выхода из строя первого элемента – 0,3, второго – 0,2, третьего – 0,4. Составить закон распределения случайной величины Х – числа вышедших из строя элементов.
Решение: случайная величина Х имеет следующие возможные значения: х1=0, х2=1, х3=2, х4=3. р1=0,3,q1=1- р1=0,7, р2=0,2, q2=1- р2=0,8, р3=0,4, q3=1- р3=0,6.
P(X=k) вычисляем по следующим формулам (см. пример 4) 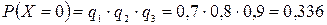 ;
;
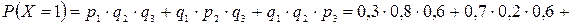
 ;
;
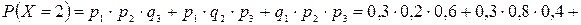
 ;
;
 .
.
Контроль: 0,336+0,452+0,118+0,024=1.
| Х | 0 | 1 | 2 | 3 |
| р | 0,336 | 0,452 | 0,118 | 0,024 |
Искомый закон распределения:
Пример 14. (Варианты 6,7)*
Среднее число заказов такси, поступающих на диспетчерский пункт в одну минуту, равно двум. Составить закон распределения случайной величины Х – числа заказов, поступающих за 4 минуты. Найти М(X), D(X).
Решение: Поток заказов на такси можно считать простейшим, т. е. обладающим стационарностью, «отсутствием последствия» и ординарностью. Интенсивность потока (среднее число событий появляющихся в единицу времени) l=2. Вероятность появления k событий простейшего потока за время t=4 определяется формулой Пуассона  , для данной задачи
, для данной задачи  . Совокупность возможных значений X есть счетное множество, т.е. х1=0, х2=1, …, хk=k+1, …; тогда закон распределения случайной величины Х – числа заказов, поступающих за 4 минуты принимает вид:
. Совокупность возможных значений X есть счетное множество, т.е. х1=0, х2=1, …, хk=k+1, …; тогда закон распределения случайной величины Х – числа заказов, поступающих за 4 минуты принимает вид:
| Х | 0 | 1 | 2 | … | k | … |
| р | 
| 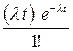
| 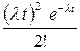
| … | 
| … |
или
| Х | 0 | 1 | 2 | … | k | … |
| р | 
| 
| 
| … | 
| … |
Воспользовавшись таблицей 3 приложения, окончательно получим:
| Х | 0 | 1 | 2 | … | k | … |
| р | 0,00035 | 0,002684 | 0,010735 | … | 
| … |
Наивероятнейшее число заказов такси за 4 минуты можно определить по получившемуся закону распределения (значения х, при которых р максимально): k¢0=7, k²0=8. Для простейшего потока событий: математическое ожидание  , дисперсия
, дисперсия 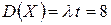 .
.
Пример 15. (Вариант 8, 9)*
| Y | 1 | 3 | 6 |
| р | 0,2 | 0,5 | 0,3 |
Даны законы распределения независимых случайных величин X и Y. Составить закон распределения случайной величины Z=X+2Y. Найти М(Z), D(Z).
| Х | -3 | 0 | 1 |
| р | 0,1 | 0,03 | 0,06 |
Решение: Закон распределения V=2Y получается из распределения Y путем умножения всех значений yi на 2. Получаем:
| V | 2 | 6 | 12 |
| р | 0,2 | 0,5 | 0,3 |
.
Для составления закона распределения случайной величины Z вычислим все ее возможные значения по формуле 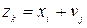 ,
, 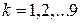 ,
, 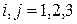 .
.
Соответствующие данным значениям 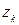 вероятности
вероятности 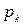 можно вычислить по формуле умножения вероятностей
можно вычислить по формуле умножения вероятностей  , т. к. события
, т. к. события  и
и  - независимы (исходим из независимости случайных величин X и Y) и наступают совместно (событие {
- независимы (исходим из независимости случайных величин X и Y) и наступают совместно (событие {  } ={совместное наступление событий
} ={совместное наступление событий  и
и  }). Тогда распределение Z принимает вид
}). Тогда распределение Z принимает вид
| Z | -1 | 3 | 9 | 2 | 6 | 12 | 3 | 7 | 13 |
| р | 0,02 | 0,05 | 0,03 | 0,06 | 0,15 | 0.09 | 0,12 | 0,3 | 0,18 |
Рассмотрим значения  . События
. События  и
и  несовместны, поэтому вероятность наступления хотя бы одного из этих событий вычисляется по правилу сложения вероятностей
несовместны, поэтому вероятность наступления хотя бы одного из этих событий вычисляется по правилу сложения вероятностей

Искомый закон распределения случайной величины Z получается после размещения zk по возрастанию.
| Z | -1 | 2 | 3 | 6 | 7 | 9 | 12 | 13 |
| р | 0,02 | 0,06 | 0,17 | 0,15 | 0,3 | 0,03 | 0,09 | 0,18 |
Математическое ожидание M(Z) и дисперсию D(Z) можно найти по формулам:
 ;
;  , где
, где  =
=  .
.
Рассмотрим другой способ.
M(Z) и D(Z) можно найти через М(Х), М(Y), D(Х), D(Y).
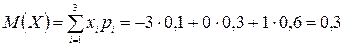

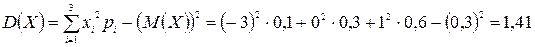

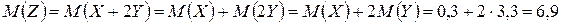 ,
,
т. к. математическое ожидание суммы равно сумме математических ожиданий слагаемых; постоянный множитель можно вынести за знак математического ожидания.
 ,
,
т. к. дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых; постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
Пример 16. (Вариант 10)*
Стрелок ведет стрельбу с вероятностью попадания в цель 0,8 при каждом выстреле. Стрельба ведется до первого попадания, но делается не более 3 выстрелов. Составить закон распределения случайной величины Х, если: а) Х – число промахов; б) Х – число попаданий; в) Х – число произведенных выстрелов.
Решение: Вероятность попадания р=0,8; вероятность промаха q=1-p=0,2.
а) Случайная величина Х – число промахов при трех выстрелах – имеет следующие возможные значения: 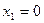 ;
; 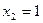 ;
;  ;
;  .
.
Событие Х=0 равносильно попаданию с первой попытки, следовательно, Р(Х=0)=р=0,8.
Событие Х=1 равносильно попаданию со второй попытки, т. е. совместному наступлению двух событий: промаха и попадания; следовательно, Р(Х=1)=q  р=0,2
р=0,2  0,8=0,16.
0,8=0,16.
Событие Х=2 равносильно попаданию с третьей попытки, т. е. Р(Х=2)=q  q
q  р=0,2
р=0,2  0,2
0,2  0,8=0,032.
0,8=0,032.
Событие Х=3 означает отсутствие попаданий, Р(Х=3)=q  q
q  q=
q=  =0,008.
=0,008.
Искомый закон распределения Х:
| Х | 0 | 1 | 2 | 3 |
| р | 0,8 | 0,16 | 0,032 | 0,008 |
б) Случайная величина Х – число попаданий – имеет следующие возможные значения: 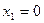 (допущено три промаха);
(допущено три промаха);  (произошло попадание с первой, второй или третьей попытки).
(произошло попадание с первой, второй или третьей попытки).
Тогда Р(Х=0)=  =
=  =0,008;
=0,008;
Р(Х=1)= р+q  р+q
р+q  q
q  р=0,8+0,16+0,032=0,992
р=0,8+0,16+0,032=0,992
или Р(Х=1)=1-Р(Х=0)=1-0,008=0,992.
Искомый закон распределения Х:
| Х | 0 | 1 |
| Р | 0,008 | 0,992 |
в) Случайная величина Х – число произведенных выстрелов – имеет следующие возможные значения:  ;
;  ;
;  .
.
Событие Х=1 равносильно попаданию с первой попытки, т. е. Р(Х=1)=р=0,8.
Событие Х=2 равносильно попаданию со второй попытки, т. е. Р(Х=2)=q  р=0,16.
р=0,16.
Событие Х=3 означает, что либо произошло попадание с третьей попытки, либо было три промаха. Тогда Р(Х=3)=q  q
q  р+q
р+q  q
q  q=0,032+0,008=0,04.
q=0,032+0,008=0,04.
Искомый закон распределения Х:
| Х | 1 | 2 | 3 |
| Р | 0,8 | 0,16 | 0,04 |
* При возникновении трудностей с построением графиков функций f(x), F(x) и многоугольника распределений смотрите пример 11.
Тема 6. Непрерывные случайные величины
Случайная величина X называется непрерывной случайной величиной, если её функция распределения (интегральная функция распределения) представима в виде
 ,
,
где f(x) – некоторая неотрицательная функция, такая что 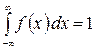 .
.
Функция f(x) называется плотностью распределения вероятностей случайной величины X (дифференциальной функцией распределения).
Примеры непрерывных распределений
1. Равномерное распределение (a<b)
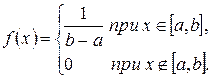 .
.
2. Нормальное распределение (s>0)
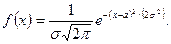
3. Показательное распределение (l>0)

Математическим ожиданием непрерывной случайной величины X называется число  ; если все возможные значения Х принадлежат интервалу (а,b), то
; если все возможные значения Х принадлежат интервалу (а,b), то  .
.
Дисперсия D(X) непрерывной случайной величины вычисляется по формуле  или
или 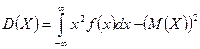 ; если все возможные значения Х принадлежат интервалу (а,b), то
; если все возможные значения Х принадлежат интервалу (а,b), то  или
или 
Вероятность того, что случайная величина X принимает значение в заданном промежутке, вычисляется по одной из формул:

Пример 17. (Варианты 2, 3, 4, 6, 7)
Случайная величина задана плотностью вероятности 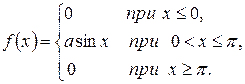
Найти: а) параметр а;
б) функцию распределения F(x);
в) вероятность попадания X в интервал 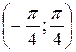 .
.
Построить графики f(x), F(x).
Решение:
а) Для нахождения параметра а воспользуемся свойствами функции f(x):
1)  2)
2) 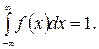
Из первого следует, что a 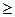 0, а из второго определяется конкретное значение а.
0, а из второго определяется конкретное значение а.
 ,
,
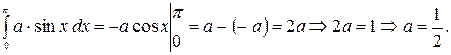
б) Для нахождения функции F(x) используем равенство 
Так как f(x) задана различным образом на трёх разных интервалах, то выражение для F(x) находим отдельно для каждого из них.
Если 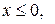 то
то 
Если  то
то 

Если  то
то  .
.
Искомая интегральная функция принимает вид
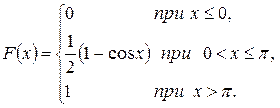
в) Вероятность попадания случайной величины X в интервал 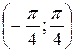 .
.
 или
или  Искомая вероятность может быть найдена иначе
Искомая вероятность может быть найдена иначе
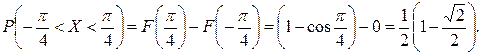
 Графики функций f(x) и F(x) показаны соответственно на Рис. 3 и Рис. 4.
Графики функций f(x) и F(x) показаны соответственно на Рис. 3 и Рис. 4.

Рис. 3 Рис.4
Пример 18. (Варианты 1, 5, 8, 9, 10)
Дана функция распределения непрерывной случайной величины X

Найти: а) плотность распределения f(x);
б) параметр а;
в) математическое ожидание M(X).
Решение:
а) Плотность распределения равна первой производной от функции распределения:

(При х=0 производная  не существует, т.к. левая и правая производные в этой точке неравны друг другу).
не существует, т.к. левая и правая производные в этой точке неравны друг другу).
б) Для нахождения параметра а пользуемся свойствами функции f(x):
 ,
, 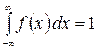 .
.


Значит, 
в) 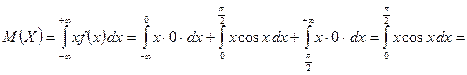
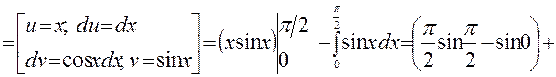

 2020-06-29
2020-06-29 162
162








