2020-06-29
81
Для вычисления определенного интеграла с помощью подстановки поступают так же, как и при вычислении неопределенного интеграла этим способом. Однако в случае определенного интеграла имеется одна особенность, на которую следует обратить внимание.
Как мы отмечали, метод подстановки заключается в том, что для приведения заданного неопределенного интеграла к табличному выражают аргумент через новую переменную, а затем находят неопределенный интеграл и полученный результат снова выражают через первоначальную перемену. В случае же определенного интеграла нет необходимости возвращаться к первоначальной переменной, однако нужно помнить, что, заменяя переменную под знаком интеграла, следует изменить и пределы интегрирования.
1. 
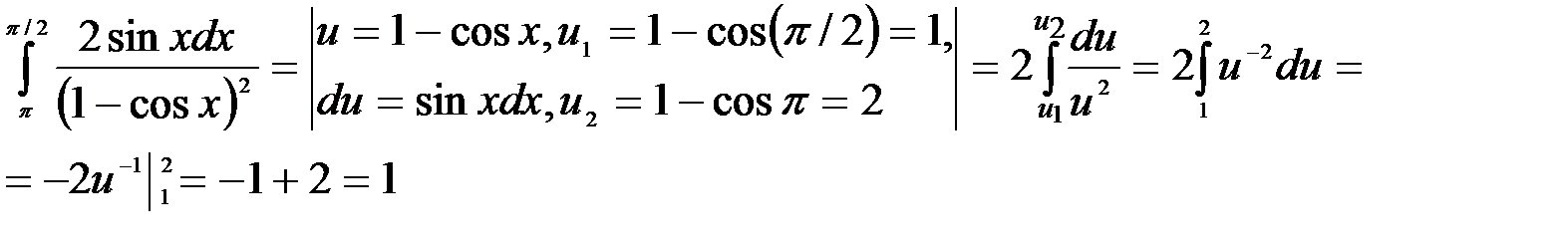
2. 
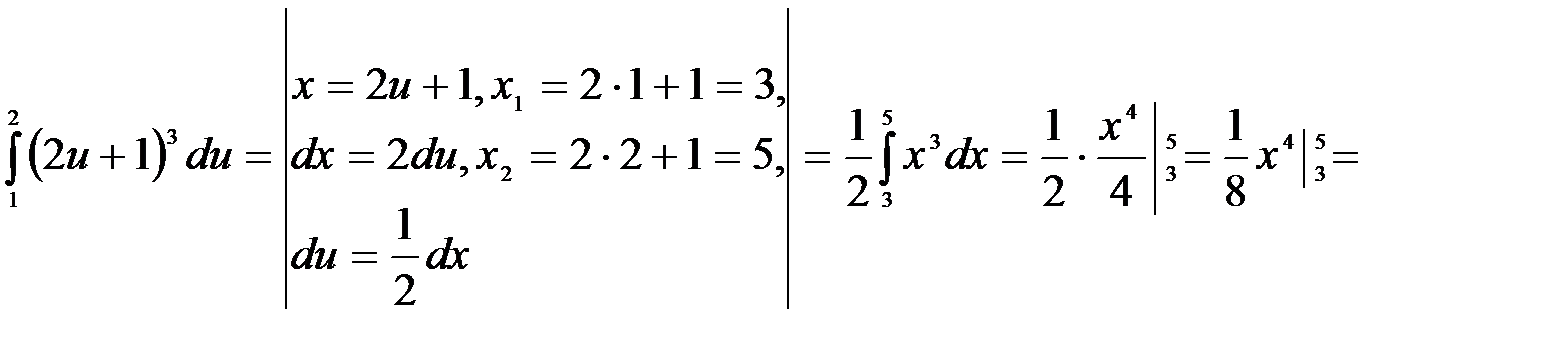
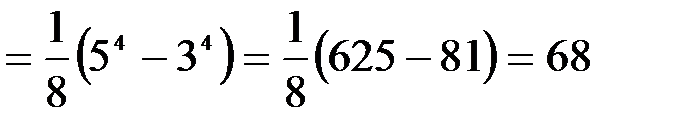
3. 
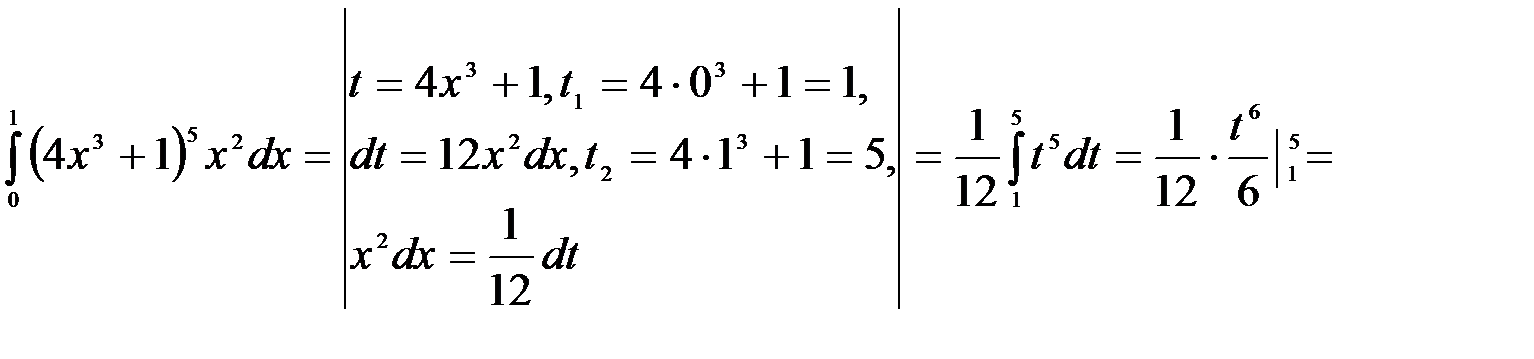
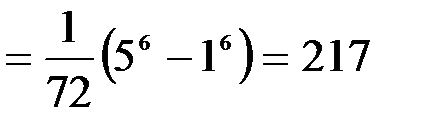
4. 
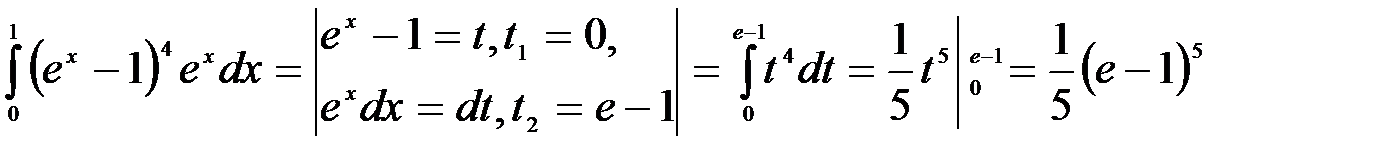
5. 
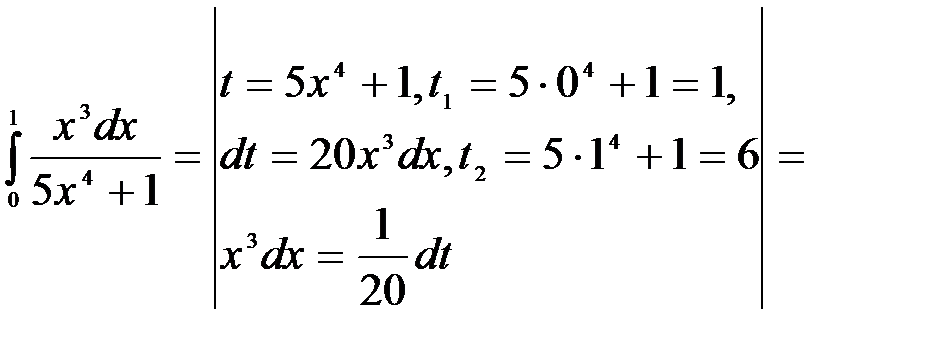
6. 
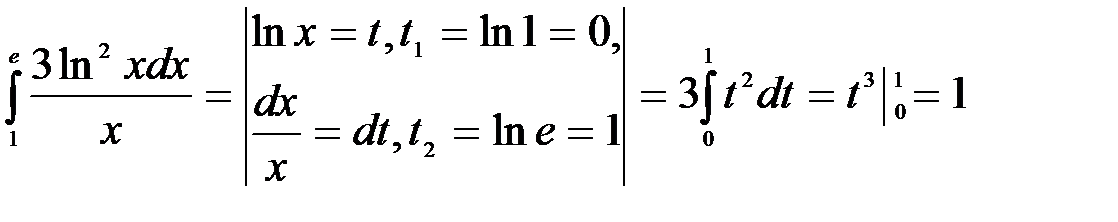
7. 
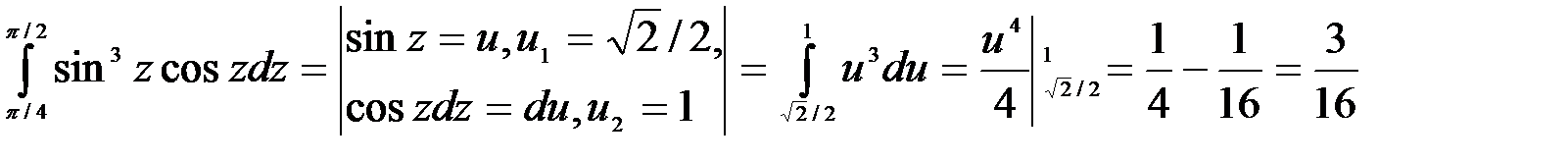
8. 
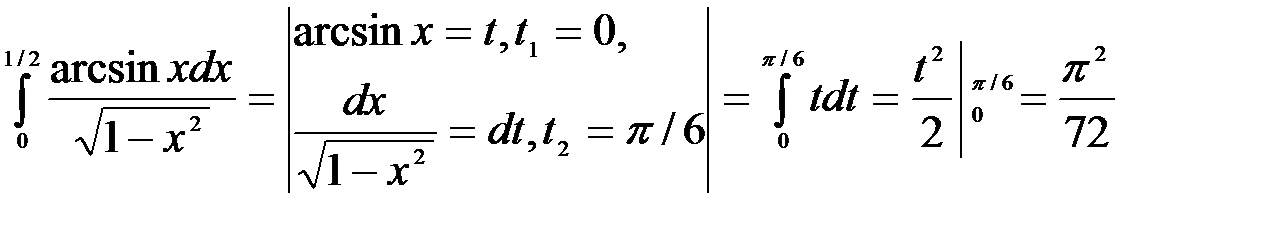
Зачетная работа по теме «Интегралы»
1. Вычислите определенные интегралы:
1) 
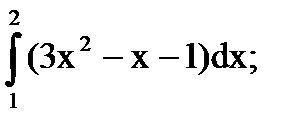2) 
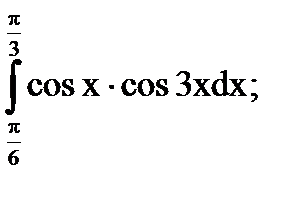
2. Вычислить неопределенные интегралы:
1) 
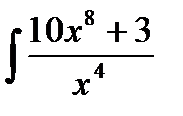; 2)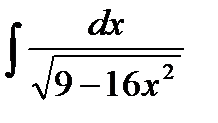 
3. Вычислить неопределенный интеграл методом подстановки (замены переменной):
1) 
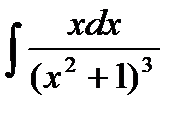; 2)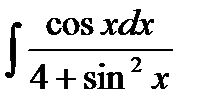 
4. Вычислить интеграл методом интегрирования по частям:
1) 
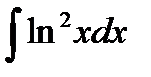2) 
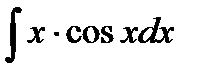
5. Найти частное решение дифференциального уравнения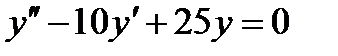 
, удовлетворяющее начальным условиям у(0)=2, 
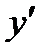(0)= -1.
