 , где С и Н – обозначение совпадения (С) или несовпадения (Н) знаков отклонений от средней признаков
, где С и Н – обозначение совпадения (С) или несовпадения (Н) знаков отклонений от средней признаков  и
и  .
.
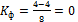 показал отсутствие связи.
показал отсутствие связи.
Измерение тесноты связи качественных признаков.
Распределение опрошенных выпускников по уровню успеваемости и намерениям продолжать учебу.
| Стратегия | Успеваемость школьников | ||||
| отл – хор | хор | хор – удовл | удовл | Итого
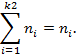
| |
| Безусловно продолжать учебу | (13,3) 16 | (26,6) 28 | (22,2) 21 | (11,9) 9 | 74 |
| условное распределение (%) | [21,6] | [37,8] | [28,4] | [12,2] | 100 |
| Скорее продолжать учебу | (3,6) 2 | (7,2) 6 | (6) 7 | (3,2) 5 | 20 |
| условное распределение (%) | [10] | [30] | [35] | [25] | 100 |
| Скорее начать работать | (0,54) - | (1,08) 1 | (0,9) 1 | (0,48) 1 | 3 |
| условное распределение (%) | - | [33,3] | [33,3] | [33,3] | 100 |
| Еще не определился | (0,56) - | (1,12) 1 | (0,9) 1 | (0,42) 1 | 3 |
| условное распределение (%) | - | [33,3] | [33,3] | [33,3] | 100 |
Итого 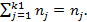 безусловное распределение
безусловное распределение 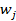 (%) (%)
| 18 [18] | 36 [36] | 30 [30] | 16 [16] | 100 |
1. Проверить гипотезу о наличии взаимосвязи между признаками (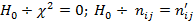 ).
).
2. Исчислить коэффициенты взаимной сопряженности Чупрова и Пирсона.
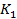 – число строк,
– число строк, 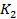 – число столбцов,
– число столбцов, 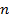 – число наблюдений,
– число наблюдений,  – частности условного распределения (в квадратных скобках),
– частности условного распределения (в квадратных скобках), 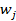 – частость итоговая в строке безусловного распределения.
– частость итоговая в строке безусловного распределения.
При независимости признаков частости условных и безусловного распределений совпадают (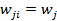 ) и
) и 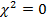 .
.
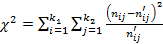 , где
, где 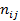 и
и 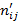 - соответственно эмпирические и теоретические частоты в
- соответственно эмпирические и теоретические частоты в  строке
строке 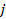 столбца.
столбца.
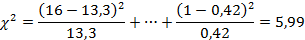
 , так
, так  ;
; 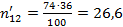 ;
; 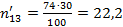 ;
; 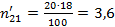 т.д.
т.д.
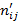 - теоретические частоты в случае отсутствия зависимости между признаками (в таблице в круглых скобках).
- теоретические частоты в случае отсутствия зависимости между признаками (в таблице в круглых скобках).
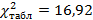 при
при 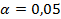 ,
, 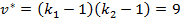 .
.
 , распределение можно считать случайным, связь не значима.
, распределение можно считать случайным, связь не значима.
Показатели тесноты связи: коэффициенты взаимной сопряженности:
Коэффициент Пирсона (С) 
Коэффициент Чупрова (К) 
Связь слабая, и т.к.  , наличие связи между признаками не доказано.
, наличие связи между признаками не доказано.
* Часто число степеней свободы означают сочетанием букв «df» (degree of freedom)
Задача 1.
Имеются данные об объеме ВВП некоторых стран и протяженности автомобильных дорог.
| ВВП, трлн долл. по ППС-2014 | млн. км | |
| США | 17,428 | 6,6 |
| Китай | 18,337 | 4,8 |
| Россия | 3,769 | 1,4 |
| Германия | 3,814 | 0,6 |
| Великобритания | 2,630 | 0,4 |
| Франция | 2,659 | 1,0 |
| Бразилия | 3,074 | 1,7 |
| Япония | 4,985 | 1,2 |
| Индия | 7,340 | 5,6 |
Найти уравнение регрессии и измерить тесноту связи на основе: линейного коэффициента корреляции и ранговых коэффициентов Спирмена и Кенделла.
Задача 2.
На основе данных об ожидаемой продолжительности жизни в некоторых странах и доли государственных расходов на здравоохранение в ВВП оценить степень тесноты связи на основе ранговых коэффициентов корреляции.
| Страна | Ожидаемая продолжительность жизни, лет | Гос. расходы на здравоохранение в % к ВВП |
| Россия | 70,2 | 3,7 |
| Германия | 80,8 | 9,0 |
| Великобритания | 81,1 | 8,1 |
| Япония | 82,7 | 1,4 |
| США | 78,7 | 8,2 |
| Австралия | 82 | 6,2 |
| Китай | 73,3 | 2,9 |
| Индия | 65,1 | 1,2 |
Задача 3.
Распределение женщин по числу рожденных детей и родительских семей по числу детей представлено в следующей таблице:
| Число детей в родительской семье | Количество женщин по числу рожденных детей | Итого | |||
| 0 | 1 | 2 | 3 | ||
| 1 | 18 | 40 | 32 | 7 | 97 |
| 2 | 49 | 90 | 70 | 14 | 223 |
| 3 | 40 | 100 | 150 | 60 | 350 |
| Всего | 107 | 230 | 252 | 81 | 670 |
1. На основе критерия χ 2 оценить значимость расхождений частот эмпирических и теоретических;
2. Оценить степень тесноты связи на основе коэффициентов Пирсона и Чупрова.
Задача 4.
На основе опроса телезрителей получено следующее распределение по признаку запоминания рекламы:
| Купили рекламируемый товар | Не купили | Итого | |
| Запомнили рекламу | 30 | 40 | 70 |
| Не запомнили | 10 | 70 | 80 |
| Итого | 40 | 110 | 150 |
На основе коэффициентов ассоциации Юла и контингенции Пирсона оцените влияние рекламы на покупку товара.
 2020-06-30
2020-06-30 127
127








