Примеры решения задач

 

1.2.1. Убедиться, что функция 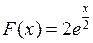 является первообразной функции  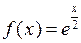на .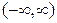

◄ Действительно, . ►

1.2.2. Убедиться, пользуясь определением, что

.

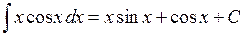◄ Так как 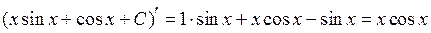, то . ►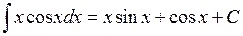

1.2.3. Вычислить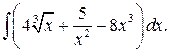

◄ При вычислении этого интеграла применим свойства 2, 3 и табличный интеграл 2.

. ►

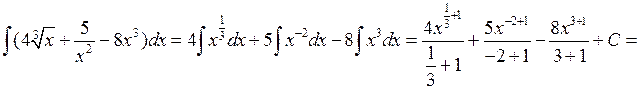
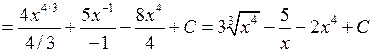1.2.4. Вычислить .

◄ При вычислении этого интеграла применим тождественные преобразования (возведение суммы в квадрат и деление суммы на число), свойства 2, 3 и табличные интегралы 2 и 3.

. ►

1.2.5.  Вычислить .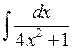

◄ При вычислении этого интеграла применим тождественные преобразования, свойство 2 и табличный интеграл 11

= . ►

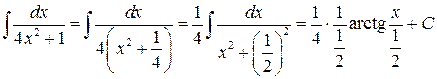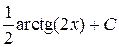1.2.6.  Вычислить .

◄ При вычислении интеграла применим тождественные преобразования, свойство 2 и табличный интеграл 12.

. ►

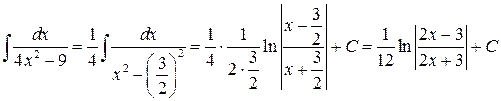1.2.7. Вычислить .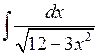

◄ Используем тождественные преобразования, свойство 2 и табличный интеграл 10.

. ►

1.2.8. Вычислить определенный интеграл .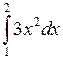

◄ Так как 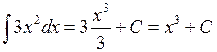, то по формуле Ньютона – Лейбница

. ►

1.2.9.  Вычислить определенный интеграл .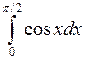

◄ Используем формулу Ньютона-Лейбница и формулу 7 таблицы интегралов: . ►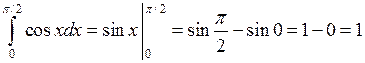

1.2.10. Вычислить определенный интеграл .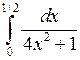

◄ Соответствующий неопределенный интеграл вычислен в примере 1.2.5. Поэтому

. ►

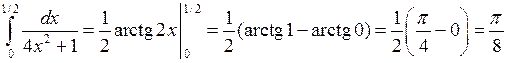1.2.11. Вычислить определенный интеграл .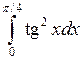

◄ Используем тригонометрическую формулу 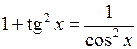, свойство линейности определенного интеграла, табличные интегралы 1 и 8 и формулу Ньютона–Лейбница:

. ►

 

Метод замены переменных

Сведения из теории

 

Существует два варианта этого метода.