Предположим, что подынтегральное выражение удалось представить в виде  (это преобразование называется подведением функции
(это преобразование называется подведением функции  под знак дифференциала d). Тогда
под знак дифференциала d). Тогда
 ,
,
где после вычисления интеграла, стоящего в правой части этой формулы, надо заменить переменную u на функцию  . Интеграл, получившийся в результате такого преобразования, может оказаться «проще» исходного, например, табличным.
. Интеграл, получившийся в результате такого преобразования, может оказаться «проще» исходного, например, табличным.
Для определенного интеграла формула имеет вид
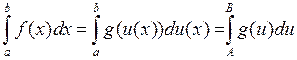 ,
,
где  ,
,  . Таким образом, при замене переменных в определенном интеграле меняются пределы интегрирования, зато не надо после интегрирования возвращаться к прежней переменной.
. Таким образом, при замене переменных в определенном интеграле меняются пределы интегрирования, зато не надо после интегрирования возвращаться к прежней переменной.
Метод подстановки
Пусть функция  дифференцируема и имеет дифференцируемую обратную
дифференцируема и имеет дифференцируемую обратную 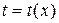 . Тогда
. Тогда
 ,
,
где после вычисления интеграла, стоящего в правой части этой формулы, надо заменить переменную t на функцию  .
.
При удачном выборе подстановки  интеграл, стоящий в правой части формулы, может оказаться «проще» исходного.
интеграл, стоящий в правой части формулы, может оказаться «проще» исходного.
Для определенного интеграла соответствующая формула имеет вид
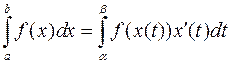 ,
,
где  , а
, а 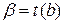 .
.
Примеры решения задач
Далее знак  будет означать ссылку на табличный интеграл с номером N.
будет означать ссылку на табличный интеграл с номером N.
2.2.1. Вычислить  .
.
◄ Перепишем интеграл в виде  . Под знаком интеграла стоит степень функции
. Под знаком интеграла стоит степень функции  , поэтому удобно подвести
, поэтому удобно подвести  под знак дифференциала:
под знак дифференциала:

 . ►
. ►
2.2.2. Вычислить  .
.
◄ Подведём под знак дифференциала  : так как дифференциал
: так как дифференциал 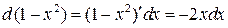 , то
, то  Поэтому
Поэтому

 .
.
2.2.3. Вычислить 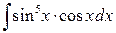 .
.
◄ Так как  и
и  . ►
. ►
2.2.4. Вычислить  .
.
◄ Так как 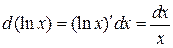 , то
, то  . ►
. ►
2.2.5. Вычислить 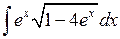 .
.
◄ Так как 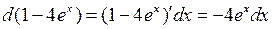 , то
, то  . Тогда
. Тогда 
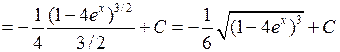 . ►
. ►
2.2.6. Вычислить 
 .
.
◄ Подведём под знак дифференциала  :
:
 . ►
. ►
2.2.7. Вычислить  .
.
◄ Так как  , то
, то 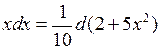 , тогда
, тогда

 . ►
. ►
2.2.8. Вычислить  .
.
◄ Так как 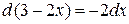 , то
, то
 . ►
. ►
2.2.9. Вычислить  .
.
◄  . ►
. ►
2.2.10. Вычислить  .
.
◄ 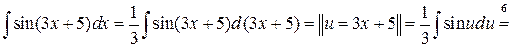

 . ►
. ►
2.2.11. Вычислить 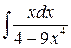 .
.
◄ 
 . ►
. ►
2.2.12. Вычислить 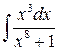 .
.
◄ 

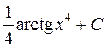 . ►
. ►
2.2.13. Вычислить  .
.
◄ Так как интеграл определенный, то будем пользоваться вариантом формулы подведения под дифференциал.



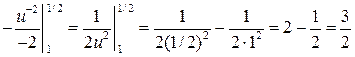 . ►
. ►
2.2.14. Вычислить  .
.
◄ 

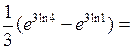
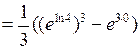
 . ►
. ►
2.2.15. Вычислить 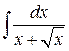 .
.
◄ Будем пользоваться формулой замены переменных в форме подстановки. Обозначим  . Тогда
. Тогда  ,
,  и
и
 . ►
. ►
2.2.16. Вычислить  .
.
◄ Так как интеграл определенный, то воспользуемся формулой замены переменных. Обозначим  . Тогда
. Тогда  при
при 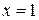 ,
,  при
при  ,
, 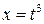 ,
, 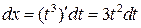 , и
, и

 . ►
. ►
 2020-06-30
2020-06-30 269
269








