Сведения из теории
6.1.1. Интегралы вида 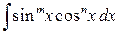 ,
,
где хотя бы одно из чисел m или n нечетное целое число
Пусть, например, 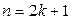 – нечетно. Тогда
– нечетно. Тогда
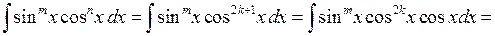
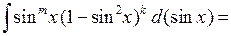 || замена
|| замена 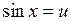 ||
|| 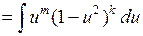 ,
,
то есть интеграл сводится к сумме табличных интегралов от степеней.
6.1.2. Интегралы вида 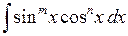 , где m и n четные целые числа
, где m и n четные целые числа
Если m и n четные целые положительные числа, то используются формулы понижения степени
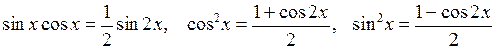 .
.
Интегралы от произведений синусов и косинусов
Различных аргументов
Для их вычисления используются тригонометрические формулы
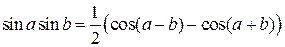 .
.
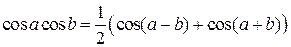 .
.
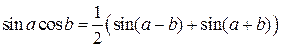 .
.
Примеры решения задач
6.2.1. Вычислить 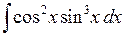 .
.
◄ Так как 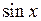 стоит в нечетной степени, то
стоит в нечетной степени, то
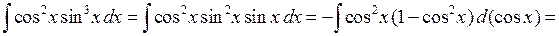
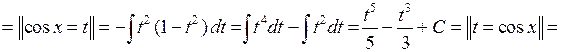
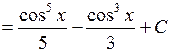 . ►
. ►
6.2.2. Вычислить 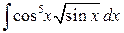 .
.
◄ Используем то обстоятельство, что косинус стоит в нечётной степени.
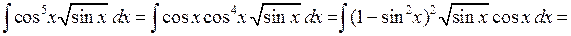
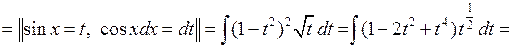
= 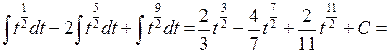
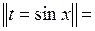
=  . ►
. ►
6.2.3. Вычислить 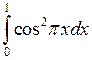 .
.
◄ Используем вторую из формул понижения степени:
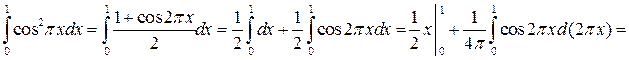
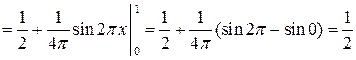 . ►
. ►
6.2.4. Вычислить 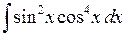 .
.
◄ Для вычисления этого интеграла от произведения синуса и косинуса в чётных степенях используем формулы понижения степени.
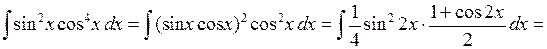
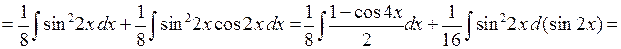
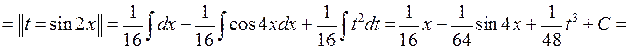
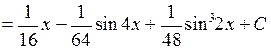 . ►
. ►
6.2.5. Вычислить 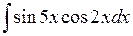 .
.
◄ Используем формулу.
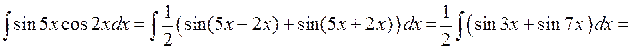
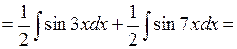
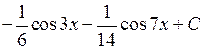 . ►
. ►
6.2.6. Вычислить 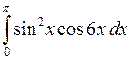 .
.
◄ Избавляемся от квадрата 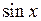 по третьей из формул понижения степени, а затем используем формулу:
по третьей из формул понижения степени, а затем используем формулу:
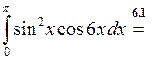
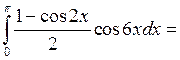
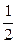
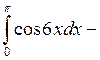
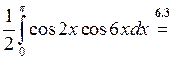

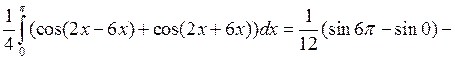
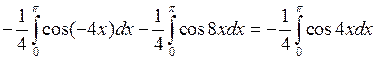
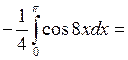
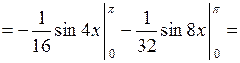
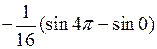
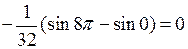 . ►
. ►
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Сведения из теории
Несобственный интеграл от функции 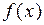 по промежутку
по промежутку 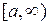 :
:
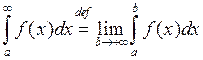 .
.
Если этот предел конечен, то говорят, что несобственный интеграл сходится, если бесконечен или вообще не существует, то несобственный интеграл расходится.
Примеры решения задач
7.2.1. Вычислить несобственный интеграл 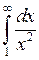 или доказать его расходимость.
или доказать его расходимость.
◄ 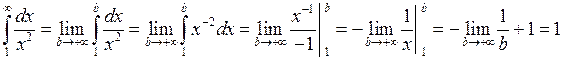 . ►
. ►
7.2.2. Вычислить несобственный интеграл 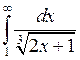 или доказать его расходимость.
или доказать его расходимость.
◄ 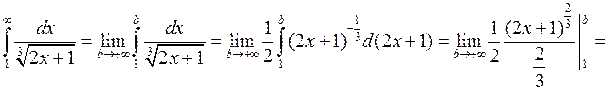
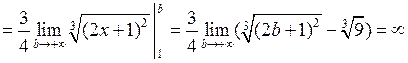 .
.
Итак, несобственный интеграл 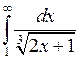 расходится. ►
расходится. ►
7.2.3. Вычислить несобственный интеграл 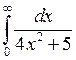 или доказать его расходимость.
или доказать его расходимость.
◄ 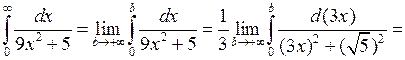 (табличный интеграл 11) =
(табличный интеграл 11) = 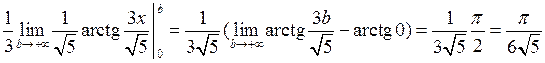 .
.
Мы учли, что 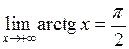 , а
, а 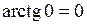 .►
.►
7.2.4. Вычислить несобственный интеграл 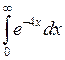 или доказать его расходимость.
или доказать его расходимость.
◄ 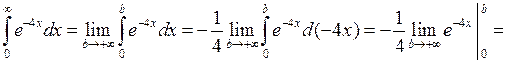
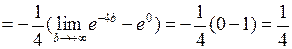 . ►
. ►
Задачи для самостоятельного решения
Вычислить несобственные интегралы или доказать их расходимость.
7.3.1. 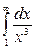 . .
| 7.3.2. 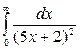 . .
|
7.3.3. 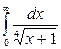 . .
| 7.3.4. 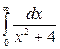 . .
|
7.3.5. 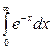 . .
| 7.3.6. 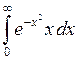 . .
|
ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛОВ
Сведения из теории
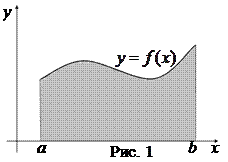
Площадь S фигуры, ограниченной линиями 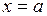 ,
, 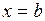 ,
, 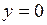 ,
, 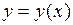 , где
, где 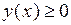 при
при 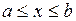 (рис. 1), находится по формуле
(рис. 1), находится по формуле
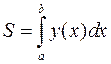 .
.
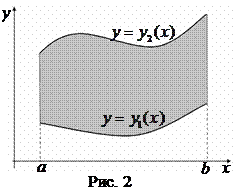 Площадь S фигуры, ограниченной линиями
Площадь S фигуры, ограниченной линиями 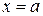 ,
, 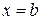 ,
, 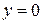 ,
, 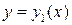 ,
, 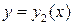 где
где 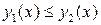 при
при 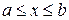 (рис. 2), находится по формуле
(рис. 2), находится по формуле
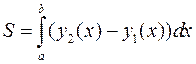 .
.
Конечно, формула (8.1) – частный случай формулы (8.2) при 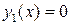 ,
, 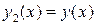 .
.
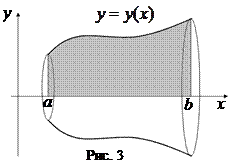 Объем тела, полученного вращением вокруг оси Ox фигуры, ограниченной линиями
Объем тела, полученного вращением вокруг оси Ox фигуры, ограниченной линиями 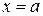 ,
, 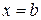 ,
, 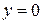 ,
, 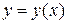 , где
, где 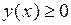 при
при 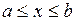 , (рис. 3) находится по формуле
, (рис. 3) находится по формуле
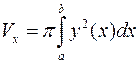 .
.
Длина дуги 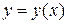 ,
, 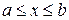 , находится по формуле
, находится по формуле
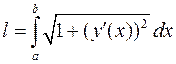 .
.
 2020-06-30
2020-06-30 248
248








