Сведения из теории
Если 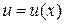 ,
,  – функции, имеющие непрерывные производные на отрезке
– функции, имеющие непрерывные производные на отрезке  , то справедлива формула интегрирования по частям для неопределенного интеграла
, то справедлива формула интегрирования по частям для неопределенного интеграла
 ,
,
или в краткой записи
 ,
,
а также формула интегрирования по частям для определенного интеграла
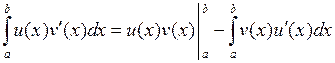
или в краткой записи
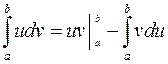 .
.
Примеры решения задач
3.2.1. Вычислить  .
.
◄ Положим  . Тогда
. Тогда  ,
,
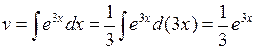 (постоянную C здесь считаем равной 0). По формуле интегрирования по частям имеем:
(постоянную C здесь считаем равной 0). По формуле интегрирования по частям имеем:


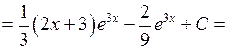

 . ►
. ►
3.2.2. Вычислить  .
.
◄ 

К стоящему справа интегралу снова применим формулу интегрирования по частям.


 . ►
. ►
3.2.3. Вычислить  .
.
◄ 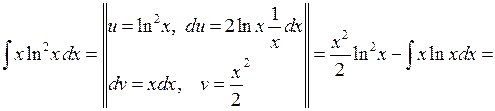
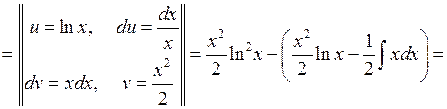

 . ►
. ►
3.2.4. Вычислить  .
.
◄ Выполним замену переменной 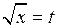 . Тогда
. Тогда  ,
, 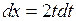 и интеграл примет вид
и интеграл примет вид

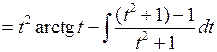
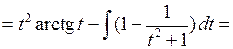

 . ►
. ►
3.2.5. Вычислить  .
.
◄ Используем формулу (3.2) интегрирования по частям для определенного интеграла.

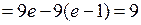 . ►
. ►
3.2.6. Вычислить  .
.
◄ 

 . ►
. ►
ПРОСТЕЙШИЕ ИНТЕГРАЛЫ,
СОДЕРЖАЩИЕ КВАДРАТНЫЙ ТРЕХЧЛЕН
Сведения из теории
Для вычисления интегралов вида
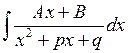
из квадратного трехчлена выделяется полный квадрат:

и делается замена переменных 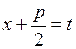 .
.
Примеры решения задач
4.2.1. Вычислить  .
.
◄ Выделим полный квадрат в квадратном трёхчлене:
 .
.
Сделаем в интеграле подстановку  . Тогда
. Тогда  ,
, 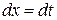 ,
,

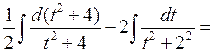
(используем табличные интегралы 3 и 11)
=  .►
.►
4.2.2. Вычислить 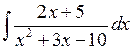 .
.
◄ Выделим полный квадрат в квадратном трёхчлене
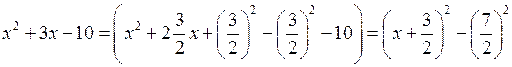 .
.


 (табличные интегралы 3 и 12) =
(табличные интегралы 3 и 12) =

 . ►
. ►
ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ
Сведения из теории
Рациональной дробью (рациональной функцией) называется отношение многочленов

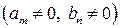 .
.
Если  , то дробь называется правильной, если
, то дробь называется правильной, если 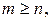 то неправильной.
то неправильной.
Рациональные дроби следующих типов называются простейшими дробями.
(1)  ; (2)
; (2) 
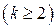 ,
,
(3)  , (4)
, (4) 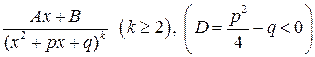 .
.
Простейшие дроби типов (1) и (2) интегрируются просто:
 ;
;
 .
.
Метод интегрирования простейших дробей типа (3) был изложен в п. 4. Интегрирование дробей типа (4) довольно громоздко и здесь излагаться не будет.
Произвольную правильную дробь можно представить в виде суммы простейших дробей. Как это сделать будет показано ниже в п. 5.2 на примерах. Поэтому интегрирование правильных дробей сводится к интегрированию простейших дробей.
С помощью деления “уголком” неправильную дробь можно представить в виде суммы многочлена (целой части) и правильной дроби (см. пример 5.2.4); тем самым интегрирование неправильной дроби сводится к рассмотренной выше задаче интегрирования правильной дроби.
 2020-06-30
2020-06-30 131
131








