2.1. Общие понятия. Теорема существования и единственности
Общий вид дифференциального уравнения первого порядка (ДУ-1)
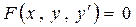 . (2)
. (2)
Если уравнение можно разрешить относительно производной, то
 , (3)
, (3)
где функция  определена в некоторой области D.
определена в некоторой области D.
Для примера рассмотрим уравнение 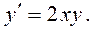 Нетрудно убедится в том, что его решением является функция
Нетрудно убедится в том, что его решением является функция  , где С - произвольная постоянная. И на любых других примерах можно убедится в том, что любое решение ДУ-1 есть бесконечное множество функций, которые определяются формулой, содержащей одну произвольную постоянную С, т.е. имеют вид
, где С - произвольная постоянная. И на любых других примерах можно убедится в том, что любое решение ДУ-1 есть бесконечное множество функций, которые определяются формулой, содержащей одну произвольную постоянную С, т.е. имеют вид
 или
или 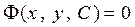 . (4)
. (4)
Определение 4. Общим решением или общим интегралом уравнения (2) или (3) называется функция (4) удовлетворяющая условиям:
1. Обращает в тождество уравнение при любых значениях С;
2. Для любой точки 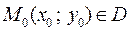 можно найти такое значение постоянной
можно найти такое значение постоянной  для которого
для которого  или
или  .
.
Давая произвольной постоянной С различные числовые значения, из общего решения получим так называемые частные решения.
Для того, чтобы из общего решения выделить конкретное частное решение, необходимо задать начальное условие, т.е. условие вида
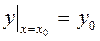 или
или  . (5)
. (5)
В этом случае задача о нахождении частного решения называется задачей Коши.
Пример 1. Решить задачу Коши: 
Как было показано, общее решение имеет вид  . Определим константу С, исходя из начального условия
. Определим константу С, исходя из начального условия
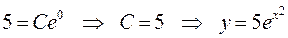 - решение задачи Коши.
- решение задачи Коши.
Теорема Коши. Если в дифференциальном уравнении  функция
функция  непрерывна в некоторой области D, содержащей точку
непрерывна в некоторой области D, содержащей точку 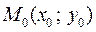 , то существует решение
, то существует решение  этого уравнения, удовлетво-ряющее начальному условию
этого уравнения, удовлетво-ряющее начальному условию  . Если, кроме этого, в этой области непрерывна производная
. Если, кроме этого, в этой области непрерывна производная 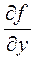 , то решение уравнения единственно.
, то решение уравнения единственно.
Пример 2. Найти область единственности решения ДУ
 .
.
Здесь  . Тогда
. Тогда

и при 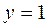 возможно нарушение единственности решения. Во всех остальных точках решение единственное.
возможно нарушение единственности решения. Во всех остальных точках решение единственное.
 2020-06-30
2020-06-30 92
92








