Определение 5. Уравнение вида 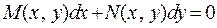 , называется уравнением в полных дифференциалах, если
, называется уравнением в полных дифференциалах, если
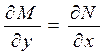 , (3)
, (3)
где частные производные непрерывны в некоторой области.
Покажем, что равенство (3) является условием полного дифферен-циала.
Теорема. Если 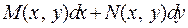 полный дифференциал некоторой функции
полный дифференциал некоторой функции 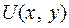 , то выполняется условие (3). Верно и обратное.
, то выполняется условие (3). Верно и обратное.
Пусть выражение 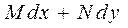 является полным дифференциалом. Это означает, что
является полным дифференциалом. Это означает, что 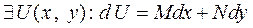 , так как
, так как
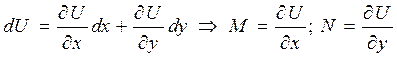 .
.
Продифференцировав первое полученное выражение по у, а второе по х, получим
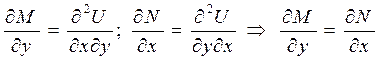 .
.
Обратно. Пусть выполняется условие (3). Требуется найти функцию 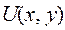 , которая должна удовлетворять условиям:
, которая должна удовлетворять условиям:
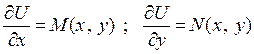 .
.
Интегрируя первое из них, получим
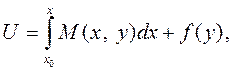
где 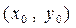 является фиксированной точкой из области определения функций
является фиксированной точкой из области определения функций 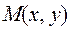 и
и 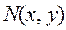 , а
, а 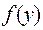 - произвольная функция. Теперь продифференцируем это выражение:
- произвольная функция. Теперь продифференцируем это выражение:
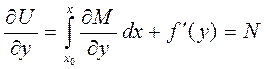
и воспользуемся условием (3)
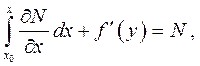
откуда
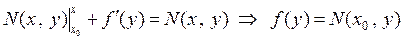 и
и 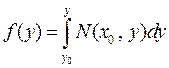 .
.
Таким образом, функция 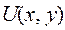 найдена
найдена
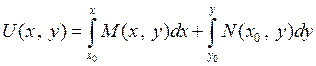 . (4)
. (4)
Теорема доказана. Возвращаемся к уравнению в полных дифферен-циалах. Если выполняется условие (3), то согласно теореме имеем
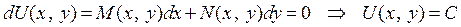 - общий интеграл.
- общий интеграл.
С учётом формулы (4) окончательно определяем общий интеграл уравнения в полных дифференциалах
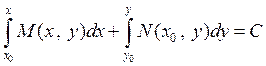 . (5)
. (5)
Пример 4. Решить задачу Коши
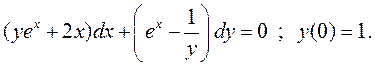
Проверим выполнение условия (3):
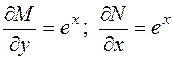 ,
,
т.е. имеем уравнение в полных дифференциалах. По формуле (5) получаем
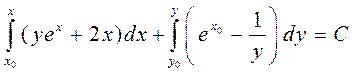
или
 .
.
Приведём подобные члены и соберём все константы в одну:
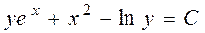 .
.
Значение константы С определим из начального условия:  .
.
Тогда решение задачи Коши будет иметь вид
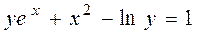 .
.
ДУ высших порядков
3.1. Определение ДУ п -го порядка
Общий вид дифференциального уравнения п -го порядка (ДУ- п):
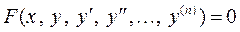 , (1)
, (1)
или разрешенного относительно старшей производной:
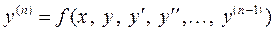 .
.
Для поиска частного решения необходимо задать начальные условия:
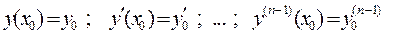 . (2)
. (2)
Определение 1. Общим решением или интегралом уравнения (1) назы-вается функция 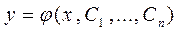 или
или 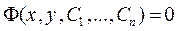 соответст-венно, которая:
соответст-венно, которая:
1. Удовлетворяет уравнению при любых значениях произвольных посто-янных 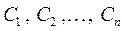 .
.
2. При любых заданных начальных условиях (2) из области определения можно найти такие 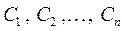 , что функция
, что функция 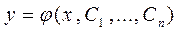 или
или 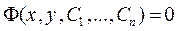 соответственно будет удовлетворять условиям (2).
соответственно будет удовлетворять условиям (2).
3.2. Уравнения, допускающие понижение порядка
3.2.1. 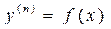 .
.
Для нахождения решения данного уравнения необходимо проинтегри-ровать его п раз.
Пример 1. Найти общее решение уравнения 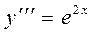 .
.
Проинтегрируем уравнение три раза:
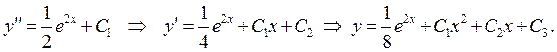
3.2.2. 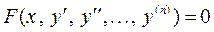 (нет у).
(нет у).
При помощи замены 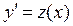 уравнение принимает вид
уравнение принимает вид
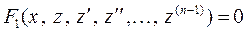 .
.
Пример 2. Найти общее решение уравнения 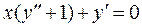 .
.
После замены 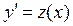 уравнение принимает вид
уравнение принимает вид
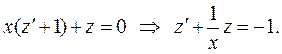
Это линейное уравнение, поэтому используем подстановку 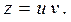
Тогда получим
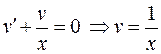
и
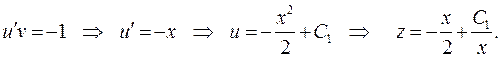
Так как 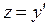 , то
, то
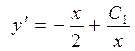 .
.
Интегрируя, окончательно получаем
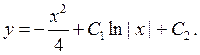
3.2.3. 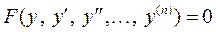 (нет х).
(нет х).
При помощи замены 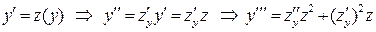 …
…
уравнение принимает вид
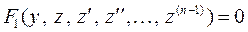 .
.
Пример 3. Решить задачу Коши 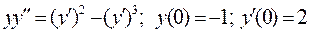 .
.
После замены 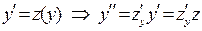 получим уравнение с разде-ляющимися переменными:
получим уравнение с разде-ляющимися переменными:
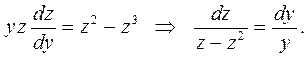
Проинтегрируем:
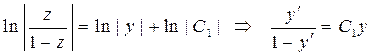 .
.
Воспользуемся начальными условиями
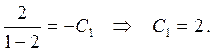
Разрешим уравнение относительно 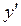 и разделим переменные
и разделим переменные
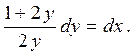
Проинтегрируем
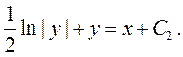
Из начальных условий находим 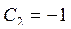 и, окончательно, получаем частное решение
и, окончательно, получаем частное решение
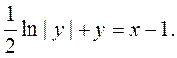
 2020-06-30
2020-06-30 104
104








