Линейные неоднородные дифференциальные уравнения второго порядка

Общий вид линейного неоднородного дифференциального уравнения второго порядка (ЛНДУ-2)

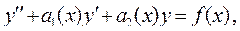                               (6)

где функции 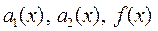 непрерывны на некотором отрезке .

Ему соответствует однородное уравнение

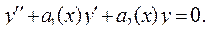                              (7)

Пусть известно общее решение уравнения (7)

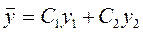.                                       (8)

Теорема (о структуре общего решения ЛНДУ-2). Общее решение ЛНДУ-2 является суммой частного решения 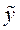 уравнения (6) и общего решения  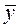соответствующего однородного (7).

Вначале покажем, что 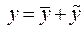 является решением уравнения (6), для чего подставим его в уравнение (6) и сгруппируем члены

.

Сумма первых трёх членов левой части равенства равна нулю, так как 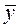 - общее решение однородного уравнения, а сумма остальных трёх членов равна 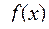, так как  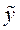- есть частное решение уравнения (6).

Таким образом, 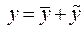  является решением уравнения (6).

Теперь покажем, что для любых начальных условий вида 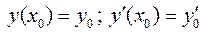 можно найти значения  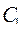и 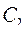, при которых решение удовлетворяло бы им. Подставим решение 

в эти условия, тогда получим систему

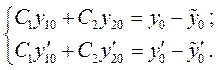                                  (9)

Система (9) является линейной системой для определения 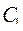 и 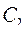 с определителем

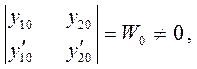
так как  и 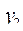 - ЛНЗ решения уравнения (7). Из решения системы (9) определяем  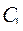и 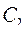. Таким образом,  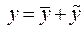является общим решением уравнения (6).

Замечание. Если 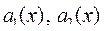 - функции от х, то не существует общих методов интегрирования уравнений (6) и (7). Рассмотрим случай, когда известно общее решение соответствующего однородного уравнения.