Рассмотрим ДУ-1 (3). Если 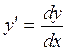 , то уравнение (3) можно пред-ставить в виде
, то уравнение (3) можно пред-ставить в виде
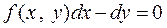 .
.
Если к тому же
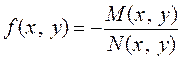 ,
,
то
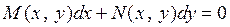 . (6)
. (6)
Пусть в уравнении (6) выполняются условия:
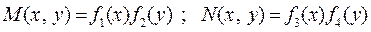 ,
,
тогда оно примет вид
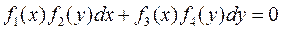 . (7)
. (7)
Определение 5. Уравнение (7) называется уравнением с разделяющи-мися переменными.
Разделим уравнение (7) на произведение 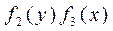 , тогда получим
, тогда получим
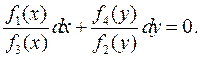 (8)
(8)
Интегрируя уравнение (8), получим его общий интеграл
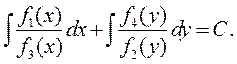 (9)
(9)
Замечание 2. Особого внимания требуют точки, где обращаются в нуль функции 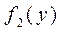 и
и 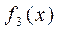 . Пусть, например,
. Пусть, например, 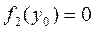 . Тогда уравнение (7) наряду с решением (9) имеет и решение
. Тогда уравнение (7) наряду с решением (9) имеет и решение  . Аналогично, если
. Аналогично, если 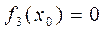 , то
, то 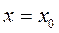 является решением уравнения (7).
является решением уравнения (7).
Пример 3. Найти общее решение уравнения 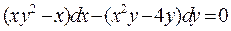 .
.
Преобразуем уравнение:
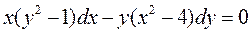
или
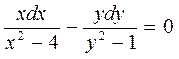 ,
,
при этом  . Интегрируя уравнение, получим
. Интегрируя уравнение, получим
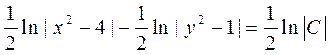
или

К этому решению нужно добавить решение вида 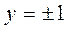 , а решение вида
, а решение вида 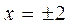 входит в общее решение при
входит в общее решение при 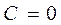 . Окончательно, имеем
. Окончательно, имеем
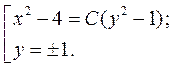
Пример 4. Решить задачу о радиоактивном распаде вещества:
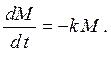
Разделим переменные: 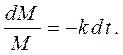
Интегрируя, получим
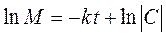 или
или 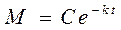 .
.
Если известна начальная масса M 0 при 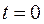 , тогда
, тогда
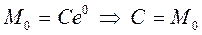 и
и 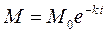 .
.
Определим коэффициент k из наблюдений. Пусть за время t 1 масса вещества стала равной M 1. Тогда
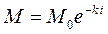 или
или 
Таким образом, получили конкретный вид закона изменения заданной массы радиоактивного вещества в зависимости от времени.
Однородные уравнения
Определение 1. Функция 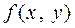 называется однородной функцией, если
называется однородной функцией, если 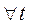 выполняется
выполняется 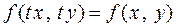 .
.
Например, функция 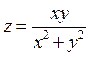 является однородной, так как
является однородной, так как
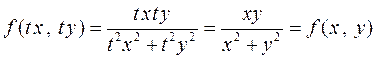 .
.
Определение 2. Уравнение вида  называется однородным уравнением, если
называется однородным уравнением, если  однородная функция.
однородная функция.
Покажем, что решение однородного уравнения сводится к решению уравнения с разделяющимися переменными.
По условию 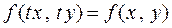 . Положим в этом тождестве
. Положим в этом тождестве 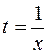 , тогда
, тогда
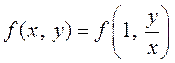
и уравнение примет вид
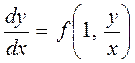 .
.
Сделаем замену 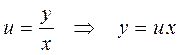 и
и 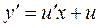 .
.
Тогда получим уравнение с разделяющимися переменными
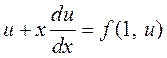 или
или 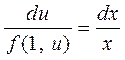 .
.
Интегрируя его, а затем, подставляя 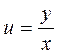 , находим решение.
, находим решение.
Замечание. Аналогично, как и для уравнений с разделяющимися переменными, если  , то однородное уравнение обладает решением
, то однородное уравнение обладает решением 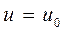 или
или 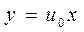 .
.
 Пример 1. Определить кривую, проходящую через точку
Пример 1. Определить кривую, проходящую через точку 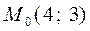 , если подкасательная АВ любой её точки есть среднее арифметическое координат.
, если подкасательная АВ любой её точки есть среднее арифметическое координат.
Если 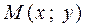 - текущая точка у
- текущая точка у
кривой, то по условию задачи,
получаем уравнение 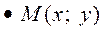
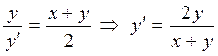 у
у
Получили однородное урав- 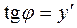
нение, поэтому сделаем замену О А В х
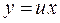 и
и 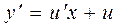 .
.
Тогда уравнение примет вид
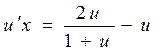 .
.
Разделяем переменные
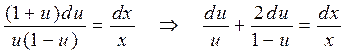
и интегрируем
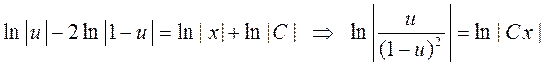 .
.
Выполнив обратную замену 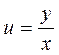 , имеем
, имеем
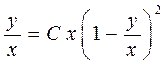 .
.
Окончательно, учитывая, что кривая проходит через заданную точку и подставляя в общее решение ее координаты
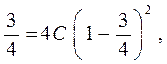
находим 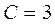 и получим искомое уравнение кривой
и получим искомое уравнение кривой
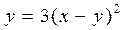 .
.
2.4. Линейные уравнения первого порядка (ЛУ–1)
Определение 3. Уравнение вида 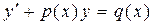 , где
, где 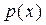 и
и 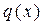 непрерывные на
непрерывные на 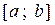 функции, называется линейным.
функции, называется линейным.
Его решение будем искать в виде
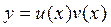 . (1)
. (1)
Продифференцируем выражение (1), а, затем подставим в ЛУ-1, получим
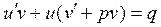 . (2)
. (2)
Функцию 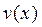 выберем из условия
выберем из условия
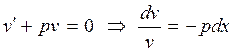 .
.
Проинтегрируем это уравнение
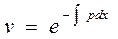 .
.
Тогда уравнение (2) примет вид
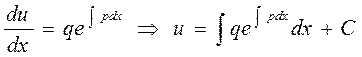 .
.
Окончательно, имеем
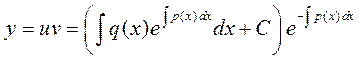 .
.
Пример 2. Найти общее решение уравнения 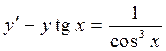 .
.
Решение ищем в виде 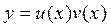 . Тогда для функции
. Тогда для функции 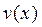 получаем уравнение
получаем уравнение
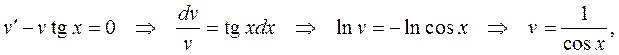
а для функции 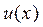 -
-
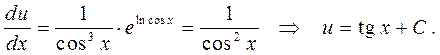
Окончательно, имеем
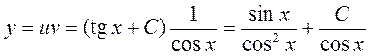 .
.
Уравнения Бернулли
Определение 4. Уравнение вида 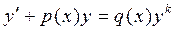 , где
, где 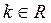 , называется уравнением Бернулли.
, называется уравнением Бернулли.
Отметим, что при 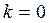 оно становится линейным, а при
оно становится линейным, а при 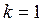 - уравнением с разделяющимися переменными. Поэтому в дальнейшем эти случаи не рассматриваем.
- уравнением с разделяющимися переменными. Поэтому в дальнейшем эти случаи не рассматриваем.
Покажем, что уравнение Бернулли путём замены 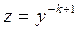 , приводится к линейному. Действительно,
, приводится к линейному. Действительно,
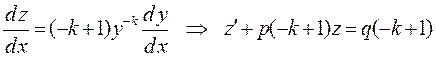 .
.
Таким образом, уравнения Бернулли интегрируются аналогично как линейные.
Пример 3. Найти общее решение уравнения 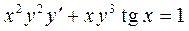 .
.
Разделим данное уравнение на 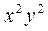 и получим уравнение Бернулли
и получим уравнение Бернулли
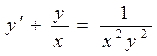 .
.
Здесь 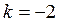 . Решение ищем в виде
. Решение ищем в виде 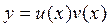 . Тогда
. Тогда
 .
.
Для функции 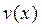 получаем уравнение
получаем уравнение
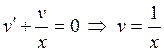 ,
,
а для функции 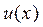 -
-
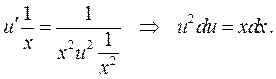
Проинтегрируем это уравнение, тогда 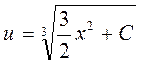 .
.
Таким образом, общее решение имеет вид
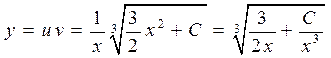 .
.
 2020-06-30
2020-06-30 91
91








