Статистические операции

В теоретической статистике большое значение имеет математическое ожидание. Но в прикладном применении эта величина трудно- или вообще невычислима так как неизвестны вероятности, поэтому все статистические характеристики вычисляются через среднее значение, которое грубо можно соотнести с математическим ожиданием.

Среднее значение

Формула: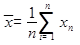

Например, для вектора последовательных значений X из 10 элементов среднее вычисляется:

X = [1:10];     % Вектор из 10 элементов (1х10)

[row col] = size(X); % Определение числа элементов

sum_value = 0;     % Инициализация переменной

for i = 1: col    % Цикл по числу элементов

sum_value = sum_value + X(i); % Суммирование

end

mean_value = sum_value / col % Вычисление арифм. среднего

Результат:

ans =

5.5000

Встроенная Matlab-функция mean(), которая делает то же самое:

mean_value = mean(X) % Вычисление среднего значения

Результат:

ans =

5.5000

 

Стандартное отклонение

Формула: 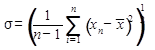. Ещё называется среднеквадратическим отклонением, хотя в теории разница всё же существует.

Вычисление для того же вектора Х и вычисленного среднего значения mean_value:

std_value = 0;

for i = 1: col

std_value = std_value + (X(i) - mean_value)^2;

end

std_value = (std_value / (col-1))^(0.5)

Результат:

ans =

3.0277

Встроенная Matlab-функция std(), которая делает то же самое:

std_value = std(X) % Вычисление стандартного отклонения

Результат:

ans =

5.5000

 

Дисперсия

Формула: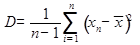

Отличается от среднеквадратического отклонения только отсутствием корня, т.е. ср.кв.отклонение = корень квадратный из дисперсии.

disp_value = 0;

for i = 1: col

disp_value = disp_value + (X(i) - mean_value)^2;

end

disp_value = disp_value / (col-1)

По этому коду есть одно замечание: для того, чтобы получить суммирование в цикле, необходимо на каждой итерации результат суммировать с этой же переменной суммы. Однако, ежели её не объявить заранее, то при первой итерации произойдёт суммирование с необъявленной переменной (вернее не произойдёт, компилятор выдаст ошибку). Поэтому во всех случаях, когда производится суммирование в цикле переменную необходимо объявлять до цикла.

 

Ковариация

Ковариация используется при анализе двух случайных величин (например x(k) и y(k)). Смысл величины в том, что она показывает "взаимную вариацию" двух различных случайных величин, где вариация - характеристика, почти совпадающая со стандартным отклонением, но без возведения в квадрат.

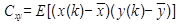
где E - математическое ожидание (в программе вычисляем как среднее значение).

Добавим второй вектор Y, от 2 до 20 в интервалом 2, чтобы длина вектора X и Y была одинаковой:

Y = [2:2:20]; % второй вектор

meanX = mean(X); % среднее значение Х

meanY = mean(Y); % среднее значение Y

Теперь ковариация между X и Y вычисляется как:

covar_xy = 0; % объявление заранее, нужно

for k=1:10   % цикл по числу элементов в векторах

covar_xy=covar_xy+(X(k)-meanX)*(Y(k)-meanY);

end

covar_xy = covar_xy / 10; % делим на число элементов

 

По формуле видно, что ковариация между X и Y равна ковариации между Y и Х. Также ковариация между X и X будет равна дисперсии переменной Х, то же самое справедливо и для Y.

Стандартная Matlab-функция, вычисляющая ковариацию: cov(X,Y).

cov(X,Y);

возвратит матрицу 2 на 2, где первый столбец - элемент (1,1) соответствует ковариации между Х и Х, элемент (1,2) - ковариации между Х и У и т.д.

Результат возращаемый функцией cov() и полученный вручную может немного отличаться (Matlab почему-то при расчёте среднего значения делит на n-1, а не на n).

Корреляция

 

 

Предобработка данных

Особенностью статистических методов является принадлежность исходных данным некоторому распределению. С точки зрения программирования это значит, что перед исследованием статистическими методами матрицы данных эту матрицу необходимо подготовить - центрировать и шкалировать данные.

 

Автошкалирование

Центрирование и шкалирование данных называют автошкалированием.

Центрирование - вычитание из всех элементов среднего значения, т.е. приведение к виду, когда среднее значение равно нулю. Для вектора достаточно просто вычесть среднее значение, оно вычтется из каждого элемента:

X_centered = X - mean_value;

Шкалирование - приведение стандартного отклонения к единице. Заключается в делении каждого элемента на среднеквадратичное отклонение вектора:

X_scaled = X_centered / std_value;

 

Для многовекторных данных, таких как данные газоаналитического датчика автошкалирование проводится отдельно для каждого сегмента (вектора).

X = Xc - repmat(mean(Xc),x_c, центрирование для двумерного массива);

 

МГК

Общий вид модели МГК:

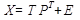, где 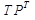- объяснённые данные, Е - шумы.

Перед расчётом исходные данные необходимо автошкалировать!

Нахождение ГК основывается на собственных векторах (eigenvector).

Собственный вектор — понятие в линейной алгебре, определяемое для квадратной матрицы или произвольного линейного преобразования как вектор, умножение матрицы на который или применение к которому преобразования даёт коллинеарный вектор — тот же вектор, умноженный на некоторое скалярное значение, называемое собственным числом матрицы или линейного преобразования.

Алгоритм NIPALS - один из распространённых методов отыскания собственных векторов, МГК обычно основывается на этом алгоритме.

http://mathprofi.ru/sobstvennye_znachenija_i_sobstvennye_vektory.html - понятное описание собственных значений и векторов.