2020-07-12
141
Розглянемо формулу 
(9.1)
(9.2)
Диференціалом функції y=f(x) називають головну лінійку по ∆x частину приросту (11.2) і записують так:
;
(9.3)
(9.4)
Застосування до наближених обчислень. Порівняння 
y з dy показє, що
Звідси
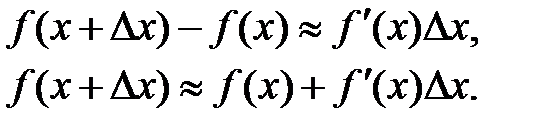
Ця формула застосовується для наближеного обчисленя значень функції при малому прирості x незалежної змінної x.
Геометричний зміст диференціала. Геометрично диференціал – це приріст ординати дотичної до кривої, проведеної в точці М(x,y).
Приклад: знайти диференціал функції 
Похідні вищих порядків
Похідною другого порядку від функції y = f(x) називається похідна від її першої похідної,тобто
і т.д.
Для похідних n -го порядку справедливі наведені нижче формули. В них покладено, що u=u(x), v=v(x), C=const.
1. 
2. 
3. 
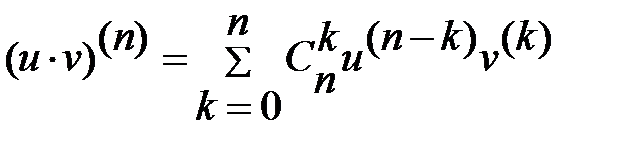- формула Лейбніца. Тут 
, 
, 
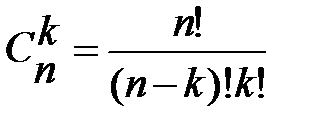
Наведемо також вирази для похідних n –го порядку від деяких функцій:
8. Функція задана неявно та її похідна. Функція, задана у вигляді рівняння F(x; y) = 0 (9.5) називається заданою неявно.
Наприклад: 
Правило знаходження похідної:
1. Знаходимо похідну лівої і правої частини, вважаючи х – аргументом 
, у – функцією від х:
у = у(х); 
2. Одержане алгебраїчне рівняння розв’язуємо відносно відомого 
:
;
Похідні вищих порядків функції, що задана неявно. Нехай функція y=f(x) задана неявно рівнянням
F(x,y)=0
Продиференціювавши обидві частини цього рівняння по змінній x, вважаючи, що y=f(x), отримаємо рівняння першого степеня відносно 
, тобто
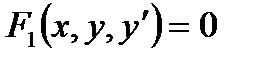
Звідси знаходимо .
Продиференціювавши обидві частини останнього рівняння по x, вважаючи, що y та функції від x,отримаємо рівняння відносно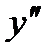 
,тобто
,
і т.д.
Похідна степенево-показникової функції.
Приклад: 
Похідна функції, заданої параметрично.
Функція, задана системою рівнянь виду 
, де t називають заданою параметрично (t – параметр).
Наприклад: 
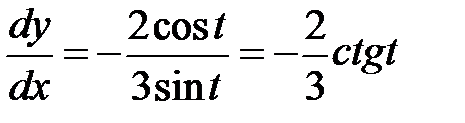
Похідна другого порядку для функції, заданої параметрично:
Висновок: 
Приклад. Знайти 
від функції, заданої параметрично 
