1. Якщо  - диференційовна функція змінних
- диференційовна функція змінних 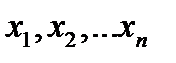 , які самі є диференційовними функціями незалежної змінної t:
, які самі є диференційовними функціями незалежної змінної t:

то похідна складної функції  обчислюється за формулою
обчислюється за формулою
 (2. 8)
(2. 8)
Зокрема, для функції двох змінних u=f(x,y) де  ,
,  ,
,
Маємо
 (1. 9.1)
(1. 9.1)
2.Якщо  - диференційовна функція змінних
- диференційовна функція змінних 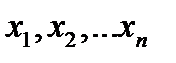 ,де
,де  ,
,  …,
…,  -диференційовні функції змінної x1 ,то маємо формулу повної похідної
-диференційовні функції змінної x1 ,то маємо формулу повної похідної
 (1.9.2)
(1.9.2)
крема, для функції трьох змінних u=f(x,y,z),де у = у(х), г = г(х), маємо формулу повної похідної
 (1.9.3)
(1.9.3)
З. Якщо  де xi =
де xi =  -диференційовані функції змінних tj ,
-диференційовані функції змінних tj ,  .
.
 (1.9.4)
(1.9.4)
Зокрема, для функції двох змінних z=f(x,y),де 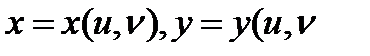 ), маємо
), маємо

(1.9.5)

Приклад 7. Знайти наближене значення функції

В точці М1(1,03 1,97).
Розв`язання. Потрібне значення заданої функції знайдено за формулою (6), Нехай М0(1,2), тоді 

Підставимо ці значення у формулу (6), що одержимо.
Z(M)=13+6*0,03+14(-0,03)=13+0,18- 0,42=12,76
| 5 |
Похідна за напрямом.Похідною функції u = f(x,y,z) заданим напрямом  в точці M0 називається границя
в точці M0 називається границя  , яка начинається
, яка начинається  або
або  Тут
Тут 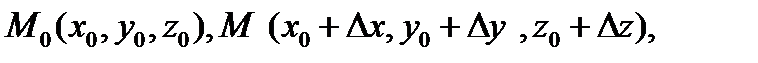

Отже, за означенням  =
=  .
.
Якщо функція диференційована,то має місце формула

де  -напрямлені косинуси вектора
-напрямлені косинуси вектора 
Аналогічно визначається похідна за напрямком для функцій двох змінних
z=f(x,y)

де 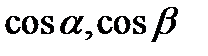 -напрямлені косинуси вектора
-напрямлені косинуси вектора  .
.
Похідна за напрямком характеризує швидкість зміни функції за даним напрямком.
Градієнт функції u=f(x,y,z) називається вектор,проекціями якого на координатні осі є відповідні частинні похідні даної функції
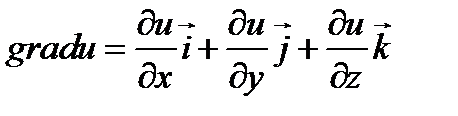
Для функцій двох змінних u=f(x,y)
 .
.
Градієнт вказує напрямок найшвидшого зростання функції в даній точці.
Похідна у напрямі градієнта має найбільше значення,тобто у напрямі  =grad u:
=grad u:

Градієнт функції в кожній точці направлений по нормалі до відповідної поверхні рівня (лінії рівня).
| 6 |
Диференціювання неявних функцій
1. Неявні функції однієї та багатьох змінних
Нехай функція  задана неявно рівнянням
задана неявно рівнянням
 ,
,
Де F диференційовна функція змінних 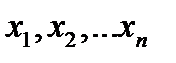 ,u. Тоді частинні похідні функції U по змінних
,u. Тоді частинні похідні функції U по змінних 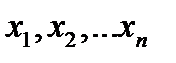 обчислюються за формулами
обчислюються за формулами
 (1.9.6)
(1.9.6)
Зокрема, якщо функція y=y(x) задано рівнянням
F(x,y)
Де F-диференційована функція змінних x,y,то
 (1.9.7)
(1.9.7)
Аналогічно,частинні похідні функції z=  заданої неявно рівнянням
заданої неявно рівнянням
F(x,y,z)=0
де F(x,y,z)-диференційована функція змінних x,y,z обчислюється за формулами:
 (1.9.8)
(1.9.8)
2. Система неявних функцій
Обмежимось розгляданням функцій двох незалежних змінних.
Нехай система двох рівнянь

Визначає u і v як диференційовані функції змінних x і y якобіан
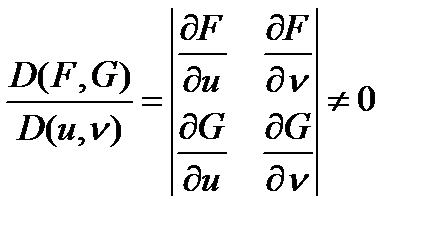
Тоді диференціали du і dv цих функцій (а отже і частинні похідні) можна знайти з системи рівнянь

Диференціювання параметрично заданих функцій
Нехай функція z незалежних змінних x i y задана параметричними рівняннями
x = x(u, v), y = y(u, v), z = z(u, v),
то

Тоді диференціал dz цієї функції (а отже, і частинні похідні)можна знайти з системи рівнянь
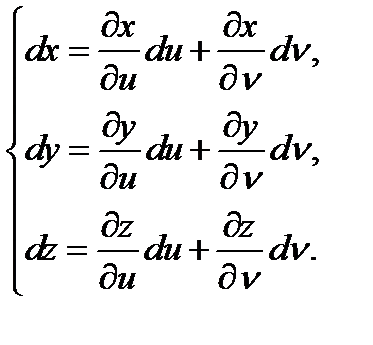
Знаючи диференціал dz = pdx+qdy, знаходимо частинні похідні
 і
і 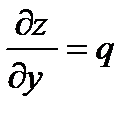 .
.
34
 2020-07-12
2020-07-12 103
103








