План
1. Монотонність функції.
2. Екстремум функції.
3. Опуклість, ввігнутість функції.
4. Точки перегину.
5. Загальна схема дослідження функції та побудова графіка.
6. Найбільше і найменше значення функції заданої на відрізку.
7. Задачі на найбільше і найменше значення.
| 1 |
Монотонність функції.
23
Означення 1.Функцію y = f (x) називають зростаючою (спадною) в проміжку (a,b), якщо більшому значенню аргумента в цьому проміжку відповідає більше (менше) значення функції, тобто якщо із нерівності х2 > x1 випливає нерівність f (x2) > f (x1), то функція f(x) – зростаюча, а якщо f (x2) < f (x1), то функція f(x) – спадна.
| a |
| У |
| 0 |
| b |
| Х |
Необхідна ознака зростання (спадання) функції.
Якщо диференційована функція зростає (спадає) в деякому проміжку, то похідна цієї функції невід’ємна (недодатня) в цьому проміжку.
Достатня ознака зростання (спадання) функції.
Якщо похідна диференційовної функції додатня всередині деякого проміжку, то функція зростає в цьому проміжку.
Якщо похідна диференційовної функції від’ємна всередині деякого проміжку, то функція спадає в цьому проміжку.
Означення 2. Зростаюча або спадна функція називається монотонною. Проміжки, в яких задана функція зростає або спадає, називають проміжками монотонності цієї функції.
Для знаходження інтервалів монотонності заданої функції y = f(x) доцільно дотримуватись такого порядку дій:
1. знайти похідну f ‘ (x);
2. знайти корені рівняння f ‘ (x) = 0;
3. визначити знак похідної f ‘ (x) в кожному із інтервалів, на які поділяється область існування функції f (x) знайденими коренями рівняння f ‘ (x) = 0;
4. за одержаними знаками похідної зробити висновок, в якому інтервалі функція зростає, а в якому спадає.
Функція y = f(x) називається монотонною на відрізку [а; b], якщо на цьому відрізку вона або зростаюча або спадна.
| а |
| х1 |
| х2 |
| b |
| f(x2) |
| f(x1) |
| X |
| Y |
| 0 |
Функція y = f(x) називається монотонною зростаючою на відрізку [а; b], якщо більшому значенню х відповідає більше значення функції х1 < х2; f(х1) < f(x2)
Функція y = f(x) називається монотонно спадною на відрізку [а; b], якщо більшому значенню х відповідає менше значення функції
х1 < х2; f(х1) > f(x2)
| а |
| х1 |
| х2 |
| в |
| У |
| Х |
| f(x1) |
| f(x2) |
| 0 0f(x2) |
Теорема 1. Якщо y = f(x) монотонно зростаюча на відрізку [а; b], то для будь-яких х з цього відрізку, похідна більша нуля.
 (10.1)
(10.1)
Якщо для будь-яких х з відрізку [а; b], коли функція спадна, похідна менша нуля.

*Приклад 1. Витрати виробництва визначені функцією
V (x) = 2x3 – 6x + 7
Знайти її інтервали монотонності.
Розв’язування. Задана функція існує при х 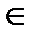 (- ∞, ∞), але має економічний зміст лише для х > 0.
(- ∞, ∞), але має економічний зміст лише для х > 0.
Знаходимо похідну: V ’ (x) = 6x2 – 6 = 6(x2 – 1).
Із 6(x2 – 1) = 0 х1 = -1, х2 = 1.
Ці значення поділяють вісь 0х на інтервали (- ∞,-1), (-1,1),(1, ∞). В кожному з цих інтервалів V ’ (x) має постійний знак.
При х  (- ∞,-1) V ’ (x) >0,
(- ∞,-1) V ’ (x) >0,
при х  (-1,1) V ’ (x) < 0,
(-1,1) V ’ (x) < 0,
при х  (1, ∞) V ’ (x) >0.
(1, ∞) V ’ (x) >0.
Отже, функція V (x) зростає при х  (- ∞,-1)U(1, ∞) і спадає в інтервалі (-1,1). З економічної точки зору, ця функція спадає в інтервалі (0,1) і зростає в (1, ∞).
(- ∞,-1)U(1, ∞) і спадає в інтервалі (-1,1). З економічної точки зору, ця функція спадає в інтервалі (0,1) і зростає в (1, ∞).
| 2 |
Означення 2. Функція f(x) має при х = х0 максимум (мінімум), якщо існує такий окіл точки х0 , для усіх точок х якого виконується нерівність
f (х0) > f (x) для максимуму,
f (х0) < f (x) для мінімуму.
Узагальненим терміном понять максимуму та мінімуму є екстремум.
| У2 |
| 0 |
| х |
| у |
| Х1 |
| Х2 |
| у1 |
Точка х1 називається точкою максимуму f (x), якщо існує такий окіл точки х1, що для будь-яких точок з цього околу значення функції менше ніж в х1: f(x) ≤ f(x1).
Точка х2 називається точкою мінімуму, якщо існує такий окіл х2, що для будь-яких точок з цього околу f(x) ≥ f(x1).
Щоб визначити, в яких з критичних точок функція має екстремум, треба застосувати достатні умови існування екстремуму.
Достатні умови екстремуму полягають у наступному:
Якщо f(x) неперервна в околі критичної точки х0 і дифереційовна в усіх точках цього околу, окрім, можливо, точки х0 , і якщо при переході х через х0 похідна змінює знак з „+” на „-”, то f(x0) = ymax; якщо у’ змінює знак з „-” на „+”, то то f(x0) = ymin; якщо у’ не змінює знака, екстремуму немає.
Теорема 2 (необхідна для екстремуму). Якщо х0 є точкою екстремуму функції y = f(x), то виконується умова 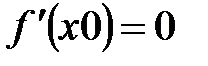 або
або  - не існує (10.2)
- не існує (10.2)
Зауваження: умова (10.2) є тільки необхідною, але не достатньою, тобто якщо ми знаємо, що точка х0 екстремальна, то умова (10.2) обов’язково виконується, але навпаки – не завжди вірно. Точки, що забороняють умову (10.2) називають підозрілі на екстремум, або критичні. Щоб знати, чи буде критична точка екстремальною потрібно дослідити достатню умову екстремуму.
Теорема 3 (достатня умова екстремуму).
Критична точка х0 буде точкою екстремуму, якщо при переході через цю точку похідна змінює знак, причому:
1) якщо похідна змінює знак „+” на „-„, то точка х1 – точка max;
2) якщо похідна функції змінює знак з „-„ на „+”, то точка х1 – min.
| х |
| у |
| 0 |
| х1 |
*Приклад 2: Знайти найбільше і найменше значення функції
y = x3 – 9x2 = 24x – 10, 0 ≤ х ≤ 3.
Розв’язання. Знаходимо критичні точки функції:
y/ = 3x2 – 18x + 24 = 0; х1 = 2, х2 = 4.
Із знайдених точок берем точку х = 2, бо 2 € [0,3].
Обчислюємо f (2) = 10, f (0) = -10, f (3) = 8. Порівнюємо числа 10, -10,8. Знаходимо minx € [0,3] y = f (0) = -10, max x € [0,3] y = f (2) = 10.
*Приклад 3: Знайти точки екстремуму та інтервали зростання та спадання такої функції:
f (х) = хе– х .
f / (х) = е– х - хе– х = е– х(1 – х)
З рівняння f / (х) = 0 знаходимо критичні точки функції f (х). У цієї функції існує одна критична точка х = 1. Так як f / (х) > 0 для х < 1 і f / (х) < 0 для х > 1, то функція f (х) зростає на проміжку [ - ∞; 1] та спадає проміжку [ 1;+ ∞]. З цього випливає, що точка х = 1 є точкою максимума функції f (х).
Відповідь: f (х) зростає на [ - ∞; 1], спадає на[ 1;+ ∞]; х = 1 - точка максимума.
У зв’язку з тим, що екстремум функції – локальний оптимум дуже часто використовується в економічній практиці, дамо схему дослідження функції на екстремум:
1. знаходять похідну f/ (х) заданої функції;
2. знаходять критичні точки першого роду (значення х, при яких f/ (х) не існує або дорівнює 0);
3. визначають знак f/ (х) в околі кожної критичної точки;
4. роблять висновок, чи має функція екстремум у знайдених точках і який саме (мінімум чи максимум);
5. обчислюють екстремальні значення функції в точках екстремуму.
Доцільно у ході дослідження використовувати таблицю.
| 3 |
Опуклість, ввігнутість функції.
Нехай f(х) диференційовна функція на інтервалі (a,b). Графік функції f(x) називається опуклим уверх або опуклим на інтервалі (a,b), якщо він розташований нижче дотичної, проведеної в будь-якій точці цього інтервалу. Графік функції f(x) називається вгнутим униз або вгнутим на інтервалі (a,b), якщо він розташований вище дотичної, проведеної в будь-якій точці цього інтервалу.
Функція y = f(x) називається ввігнутою на відрізку [а;b], якщо для будь-яких х з цього відрізка графік функції знаходиться над дотичними в даній точці х2.
y = f(x) – опукла на відрізку [а;b], якщо графік функції знаходиться під дотичною в точці х2.
Достатня умова опуклості (вгнутості) графіка функції. Нехай функція f(x) двічі диференційовнана інтервалі (a,b). Тоді, якщо:
1. f ” (х) < 0 на (a,b) , то графік функції f(x) є опуклим на (a,b);
2. f ” (х) > 0 на (a,b) , то графік функції f(x) є вгнутим на (a,b).
Із означення точки перегину та достатніх умов опуклості (вгнутості) випливає, що, коли х0 – абсциса точки перегину графіка функції у = f(x), то друга похідна дорівнює нулю, нескінченності або не існує.
| y = f(x) |
| c |
| b |
| 0 |
| a |
Означення 3. Значення х, при яких f ” (х) = 0 або не існує, називають точками другого роду функції f(x).
| 4 |
Точки перегину.
Точки, в яких графік функції змінює ввігнутість на опуклість і навпаки, називаються точками перегину.
Достатня умова точки перегину. Нехай функція f(x) двічі диференційовна в деякому околі О (х0,δ) критичної точки другого роду х0, за виключенням, можливо, самої точки х0. Тоді, якщо f ” (х) в інтервалах (х0 – δ, х0), (х0, х0 + δ) має протилежні знаки, то х0 – абсциса точки перегину. Якщо ж f ” (х) має однаковий знак у цих інтервалах, то точка з абсцисою х0 не є точкою перегину.
| 0 |
| Х |
| У |
| Х0 |
Х0 – точка перегину.
Теорема 5. Якщо функція y = f(x) вгнута на відрізку [а; б], то для будь-яких х  [а; б] друга похідна від цієї функції більша нуля.
[а; б] друга похідна від цієї функції більша нуля.
 (10.4) х
(10.4) х  [а; б]
[а; б]
Теорема 6. Якщо функція y = f(x) опукла на відрізку [а; б],то для будь-яких х  [а; б] друга похідна менше нуля.
[а; б] друга похідна менше нуля.

Теорема 7. (необхідна умова перетину).
Якщо х0 є точкою перетину функції y = f(x), то виконується умова:
 або
або  - не існує (10.4),
- не існує (10.4),
то ця точка підозріла на перетин.
Теорема 8 (достатня умова перетину)
Якщо для х0 виконана умова (10.4) і при переході через цю точку похідна змінює знак, то х0 – точка перетину.
Правило. Точка х = х0 буде точкою перегину кривої y = f(x), якщо:
1. f ” (х0) = 0 або не існує;
2. знаки f ” (х) зліва (х < х0) та справа (х > х0) різні.
Якщо f ” (х) не змінює свій знак при переході аргумента через х0, то при х = х0 перегину не буде.
Умову 1 цього правила називають необхідною умовою, а 2 – достатньою умовою існування точок перегину графіка функції.
| 5 |
Загальна схема дослідження функції та побудова графіка.
Для науково обґрунтованого дослідження функції та побудови її графіка доцільно дотримуватись такої схеми:
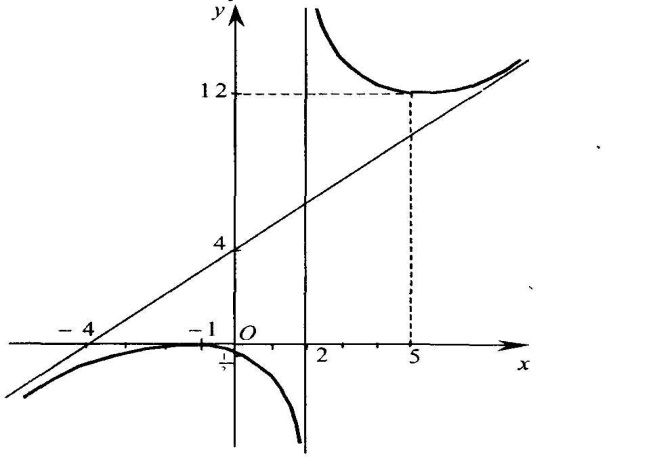
*Приклад 4. Дослідити функцію f(x) =  та побудувати її графік.
та побудувати її графік.
1. Область визначення функції D(f) = (- ∞,2) U (2,+ ∞).
На iнтервалi (- ∞,2) f(x) < 0, на iнтервалi (2,+ ∞) f(x) > 0.
2. Функція не є парною, не є непарною, бо:
f(-x) =  =
= 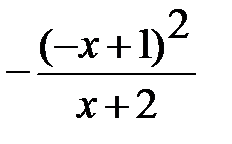 ,
,
тобто f(-x) ≠ f(x), f(-x) ≠ - f(x).
Функція неперіодична, бо не існує такого числа Т, Т > 0, щоб
F (х + Т) = f(x), Ұх є D(f).
Отже, маємо функцію загального вигляду.
3. Точки перетину з осями координат (—1,0) та (0,  ).
).
4. Точка розриву функції х = 2. Маємо розрив другого роду, бо
limx→2-0 f(x) = - ∞, limx→2+0 f(x) = + ∞.
5. Вертикальна асимптота х = 2, бо limx→2f(x) = ∞.
Похилі асимптоти шукаємо у вигляді у = kx + b.
k = limx→± ∞  = limx→± ∞
= limx→± ∞  =1.
=1.
b = limx→± ∞ [f(x) - kx] = limx→± ∞  = limx→± ∞
= limx→± ∞  =4.
=4.
Отже, у = х + 4 — похила асимптота.
6. Знаходимо точки екстремуму та визначаємо інтервали монотонності функції.
f |(x) =  =
= 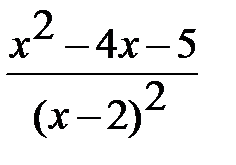 =
= 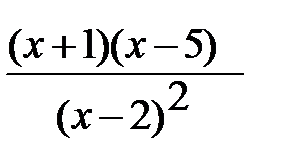 .
.
Для знаходження критичних точок розв’язуємо рівняння, f |(x) = 0,тобто (х+1)(х-5)=0, (х-2)2 ≠ 0,звiдки х1 =-1, х2 =5.
Критичні точки х1 = -1, х2 = 5 та точка х = 2 (це точка розриву функції) поділяють область визначення функції на інтервали, якi вказані на наведеній нижче схемі. На цій схемі над віссю Ох вказано знак похідної функції у’ = f |(x), пiд віссю Ох показана поведінка функції у = f(x) на вказаних інтервалах. Тут стрілками вказується, що функція зростає чи спадає. Слова max min вказують вiдповiдно точки, де функція досягає максимуму чи мiнiмуму.
| max min + - - + -1 0 2 5 х |
На проміжку (-∞, 1)U (5, +∞) функція зростає;
на промiжку (-1,2) U (2,5) функція спадає.
7. Знаходимо точки перегину графіка кривої та визначаємо інтервали опуклості та вгнутості.
f |(x) =
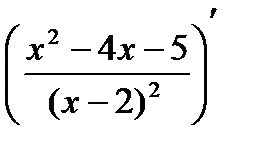 =
=  =
= 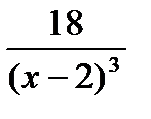
f ||(x) ≠ 0;
f ||(x) < 0 на промiжку (-∞, 2), тобто крива опукла на цьому промiжку;
f ||(x) > 0 на промiжку (2, +∞), тобто крива вгнута на цьому промiжку.
Точок перегину немає, бо точка х = 2, в околі якої змінюється знак другої похідної, є точкою розриву функції. Результати цього дослідження наведено на схемі.
| - |
| + |
0 2 х
U точка розриву ∩
Тут знак ∩ означає опуклість, знак U вгнутість.
8. Проводимо додаткові дослідження:
а) на iнтервалi(-∞,2), f(x) <0 (графік нижче осі Ох)на інтервалі (2, +∞)
f(x) > 0(графік вище осі Ох);
б) дослідимо поведінку функції на нескiнченностi:
limx→± ∞ f(x) = 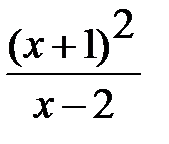 = ± ∞.
= ± ∞.
На основі дослідження поступово будуємо графік функції f(x) = 
27
| 6 |
Якщо функція f(x) неперервна на відрізку [а;b], то вона досягає на цьому відрізку своїх найбільшого та найменшого значень. Для знаходження цих значень треба:
1.Знайти всі критичні точки функції f(x) на відрізку [а;b];
2.Обчислити значення функції f(x) у критичних точках;
3. Обчислити значення функції f(x) у точках х = а, х = b;
4.Серед обчислених значень вибрати найбільше та найменше.
*Приклад 5. Знайти найбільше М та найменше m значення функції:
f(x) = х3 – 3х2 – 9х = 35 на відрізку [-4,4].
Знаходимо критичні точки даної функції, що лежать всередині [-4,4] і обчислюємо значення функції в цих точках:
F!(x) = 3х2 - 6х – 9;
3х2 - 6х – 9 = 0;
х = -1, х = 3 – критичні точки функції, що належать заданому відрізку;
f (-1) = 40, f (3) = 8.
Обчислюємо значення даної функції в точках х = -4, х = 4 – межах відрізка [-4,4]: f (-4) = -41, f (4) = 15.
З отриманих чотирьох значень вибираємо найбільше та найменше.
Отже, М = f (-1) = 40, m = f (-4) = -41.
| 7 |
Задачі на найбільше і найменше значення.
Задача № 1. Знайти такий циліндр, який мав би найбільший об’єм при заданій повній поверхні S.
Нехай радіус основи циліндра R=x, а висота H=у.
Тоді:
S= 2Sосн +Sбічн = 2пх2+2пху.
Звідси:
у=  .
.
Отже, об’єм циліндра представиться так:
V=V(x) = Sосн H= пх2  =
= 
Задача зводиться до дослідження функції V (х) на максимум при х> 0.
V !(x) = 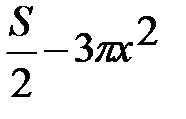 ;
;  =0;
=0; 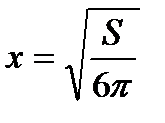 .
.
Це критична точка. Дослідимо її на екстремум.
V !!(x) = -6пх; V !! 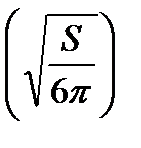 =
=  = -
= -  < 0.
< 0.
Отже, в точці 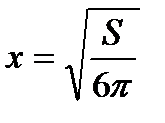 функція має максимум, тобто об’єм має найбільше значення. Висота циліндра при цьому така:
функція має максимум, тобто об’єм має найбільше значення. Висота циліндра при цьому така:
H = у=  = 2
= 2 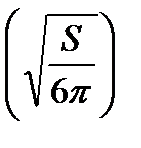 = 2R.
= 2R.
Отже, висота Н циліндра дорівнює 2R діаметру основи циліндра. За цієї умови циліндр має найбільший об’єм.
31
 2020-07-12
2020-07-12 266
266








