Якщо функція y = f(x) диференційована в деякій точці 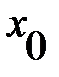 , то вона в цій точці неперервна:
, то вона в цій точці неперервна:
Доведення: якщо y = f(x) диференційована в 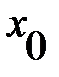 , то існує
, то існує
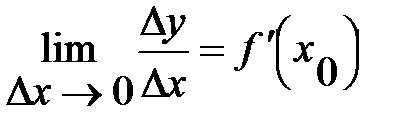
В силу того, що границя змінної величини відрізняється від самої змінної лише на нескінченно малу величину 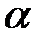 , то маємо:
, то маємо:
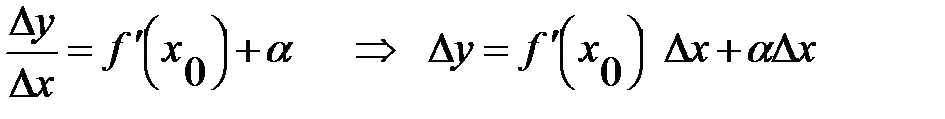
Оскільки 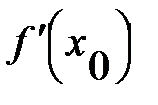 - стала, то з властивостей нескінченно малих випливае,що
- стала, то з властивостей нескінченно малих випливае,що 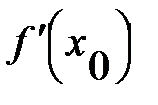 ∆x і
∆x і 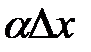 є нескінченно малими величинами. Звідси ∆у→0, коли ∆x→0, тобто функція y = f(x) неперервна в точці
є нескінченно малими величинами. Звідси ∆у→0, коли ∆x→0, тобто функція y = f(x) неперервна в точці 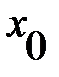 .
.
Наслідок: З цієї теореми випливає,що неперервність функції є необхідною умовою диференційованості функції. Це означає, що в точках розриву функція не має похідної, тобто вона не диференційована.
4. Основні правила диференційювання
1. Похідна постійної величини С дорівнює нулю, тобто С´=0
2. Якщо кожна із функцій 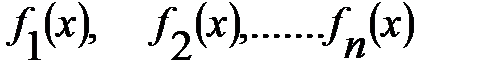 (n – нескінченне число) диференційована в деякій точці х, то її алгебраїчна сума також є диференційованою в цій точці, причому похідна алгебраїчної суми цих функцій дорівнює такій самій алгебраїчній сумі їх похідних, тобто
(n – нескінченне число) диференційована в деякій точці х, то її алгебраїчна сума також є диференційованою в цій точці, причому похідна алгебраїчної суми цих функцій дорівнює такій самій алгебраїчній сумі їх похідних, тобто
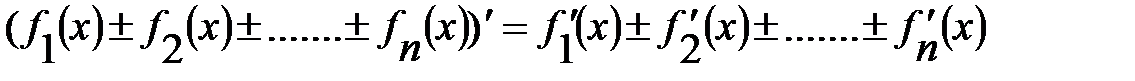
3. Якщо кожна з функцій u(x) та V(x) диференційована в точці х, то добуток цих функцій також має похідну в точці х, причому цю похідну знаходять за формулою:
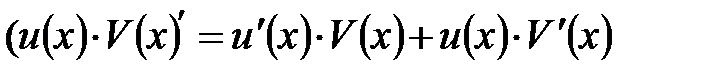
4. Якщо u(x) та V(x) мають похідні в точці х і V(x) 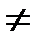 0, то частка цих функцій також має похідну в точці х, яку знаходять за формулою:
0, то частка цих функцій також має похідну в точці х, яку знаходять за формулою:
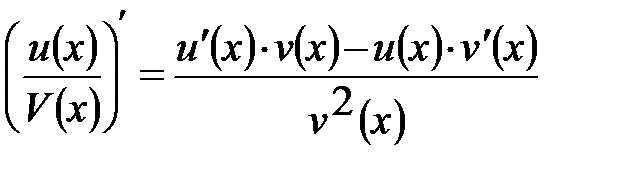
5. Якщо у=f(u), u= 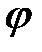 (x) і функції f та
(x) і функції f та 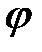 диференційовані функції своїх аргументів, то існує похідна по складної функції у, причому вона дорівнює добутку похідної функції у по проміжному аргументу u та похідної функції
диференційовані функції своїх аргументів, то існує похідна по складної функції у, причому вона дорівнює добутку похідної функції у по проміжному аргументу u та похідної функції 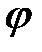 по аргументу х, тобто
по аргументу х, тобто
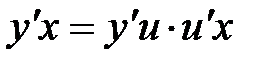
Таблиця похідних
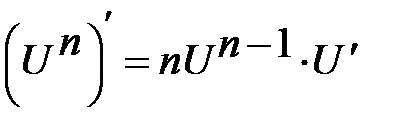
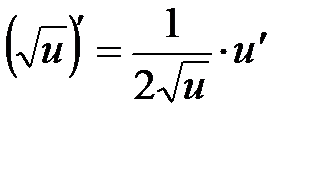
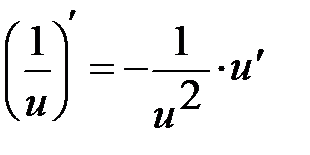
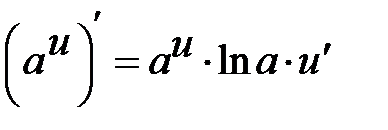
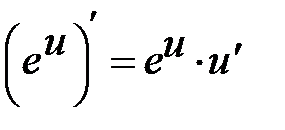
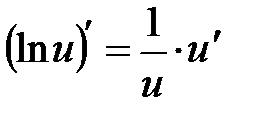
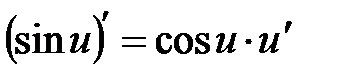
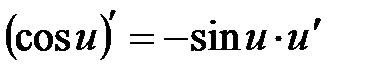
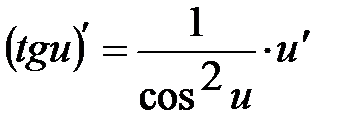
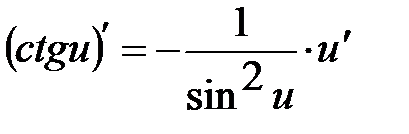
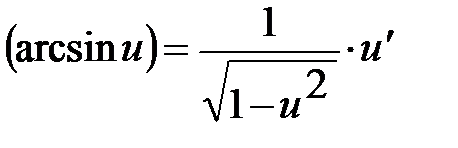
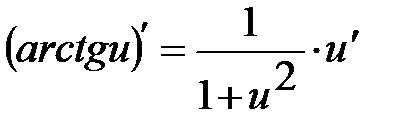
 2020-07-12
2020-07-12 104
104








