Интегрирование тригонометрических функций

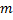1. , где  или 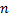 – нечетное натуральное число (например, )

Пример.

2.   , где  – четные. Используем формулы понижения степени

Пример.

3.  где (т.е.  ). Используем формулы

Пример.

4.  . Понижение показателя с использованием формул

 

Пример.  

5.  где Понижение степени с использованием формул:

 и т.д.

  Пример.

 

 +c,

Где

6.

Преобразование произведения тригонометрических функций в сумму.

7. , где  .

Подстановка .

Пример.  

8. , где .

Подстановка ,

Пример.

Интегрирование иррациональных функций.

I. .

Замена , –общий знаменатель  (Н.О.К. ).

Пример.

II.

Замена

Пример.

III. .

Выделив полный квадрат, получим интеграл одного из видов:

a)

Замена

Пример.

b) .

Замена .

Пример.

c) .

Замена

Пример.

 

 

Примеры интегралов, не выражающихся через элементарные функции:

  («неберущиеся» интегралы).

Интегрирование рациональных дробей. Разложение правильной рациональной дроби в сумму простейших. Интегрирование простейших дробей. Интегрирование неправильных рациональных дробей.

 

Рациональная дробь

где

Опр. Рациональная дробь называется правильной, если .

Опр. Рациональная дробь  называется неправильной, если .

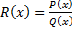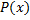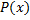Пусть  – неправильная дробь. Разделим с остатком  на , т.е. представим  в виде , где  – многочлен степени , степень многочлена  меньше 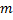. Тогда , где  – правильная рациональная дробь.

Пример.

Разложение многочлена на множители. Пусть

Тогда
              (1.3.1)

где  – корни многочлена кратности  соответственно, 

.

Пример.

.

 

Простейшие рациональные дроби.

Опр. Простейшими называют рациональные дроби одного из следующих видов:

1.

2.

3.

4.