1. ДУ с разделяющимися переменными
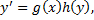
или
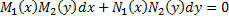 .
.
Запишем ДУ в виде 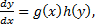
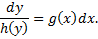
Проинтегрируем:
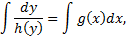
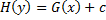 – общий интеграл,
– общий интеграл, 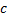 – произвольная постоянная.
– произвольная постоянная.
Замечание. Если уравнение 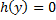 имеет корни
имеет корни  , то функции
, то функции 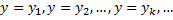 являются частными решениями ДУ.
являются частными решениями ДУ.
Пример.
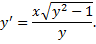
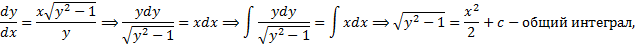
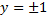 – также решение ДУ.
– также решение ДУ.
2. Однородные ДУ
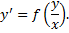
Замена 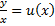 , тогда
, тогда 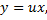
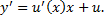
Тогда, подставляя в ДУ получим
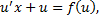
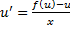 – ДУ с разделяющимися переменными, находим
– ДУ с разделяющимися переменными, находим 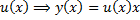 .
.
Пример.
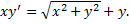
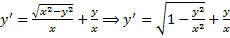 (x>0).
(x>0).
Замена: 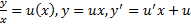 . Подставим в ДУ:
. Подставим в ДУ:
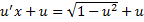 ,
,
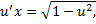
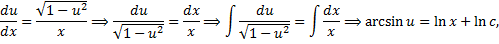
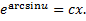
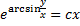 – общий интеграл.
– общий интеграл.
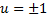 – решение, т.е.
– решение, т.е. 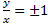 , т.е.
, т.е. 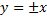 .
.
3. Линейные ДУ 1-го порядка.
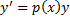 – линейное однородное ДУ (ЛОДУ) 1-го порядка.
– линейное однородное ДУ (ЛОДУ) 1-го порядка.
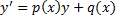 – линейное неоднородное ДУ (ЛНДУ) 1-го порядка.
– линейное неоднородное ДУ (ЛНДУ) 1-го порядка.
I. ЛОДУ 1-го порядка.
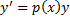 – с разделяющимися переменными
– с разделяющимися переменными
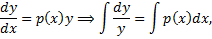
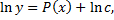
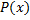 – первообразная
– первообразная 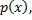
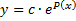
(р 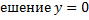 получаем при
получаем при 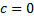 ).
).
II. ЛНДУ 1-го порядка.
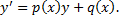
a. Решим соответствующее ЛОДУ: 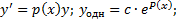
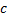 – произвольная постоянная
– произвольная постоянная
b. Решение ЛНДУ ищем методом вариации постоянной, т.е. в виде
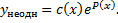
Тогда 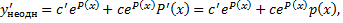
Подставим в ЛНДУ: 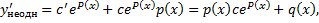
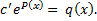
Находим 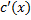 ; интегрируем, находим
; интегрируем, находим 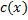 .
.
Пример.
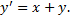
a. Соответствующее ЛОДУ: 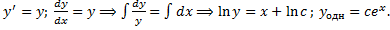
b. Ищем решение ЛНДУ в виде 
Подставляем в ЛНДУ:
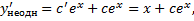
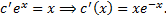
Проинтегрировав, получим
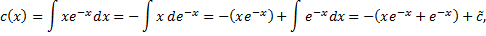

Подставим в (2.3.1):
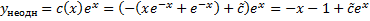 =
= 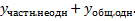
Замечание. ДУ
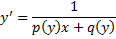
сводится к ЛНДУ относительно обратной функции 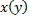
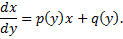
Решаем методом вариации произвольной постоянной:
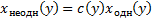 .
.
4. Уравнения Бернулли
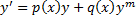 ,
,
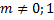 .
.
Ищем решения в виде 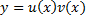 . Подставим в ДУ:
. Подставим в ДУ:
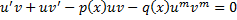 ,
,

Найдем функцию 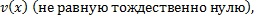 такую, что
такую, что
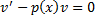 – ДУ с разделяющимися переменными (ЛОДУ).
– ДУ с разделяющимися переменными (ЛОДУ).
Используя (2.3.2), получим
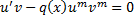
– ДУ с разделяющимися переменными. Найдем 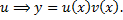
Пример.
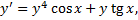
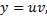
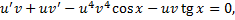
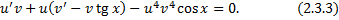
Найдем 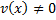 из ДУ
из ДУ 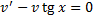 .
.
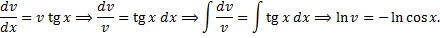
Подставим 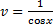 в (2.3.3):
в (2.3.3):
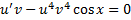 ,
,
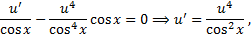
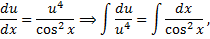
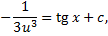
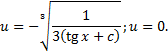
Тогда
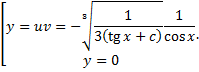
Замечание. ДУ
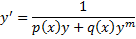
сводится к ДУ Бернулли относительно функции 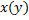 :
:
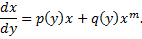
Решение ищем в виде 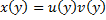
 2020-07-12
2020-07-12 942
942








