2020-07-12
2407
Пусть функции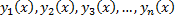 
линейно зависимы на 
. Тогда 
: 
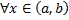Док-во: по определению линейной зависимости функций 
, не все равные 
, такие, что 
. Последовательно продифференцируем это равенство:
Зафиксируем 
(2.7.2) – СЛАУ (однородных) относительно 
, которая имеет ненулевое решение, т.е. определитель системы равен , т.е. (). 
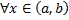Замечание. Обратное неверно, т.е. если 
, то функции могут быть линейно независимы.
Пример.
,
.
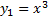Т.е. 
на 
, но 
и 
линейно независимы, т.к.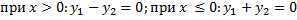 
. Не существует 
, таких, что 
для всех 
.
Теорема о вронскиане системы линейно независимых частных решений ЛОДУ
Пусть 
– линейно независимые на – частные решения ЛОДУ n-го порядка 
. Тогда 
Док-во: (от противного)
Пусть 
. Рассмотрим СЛАУ относительно :
Ее определитель 
, следовательно, система имеет ненулевое решение, т.е. , не все равные , такие, что выполняется система (2.7.3).
Рассмотрим частное решение ЛОДУ .
.
Оно удовлетворяет в т. 
начальным условиям (в силу (2.7.3)):
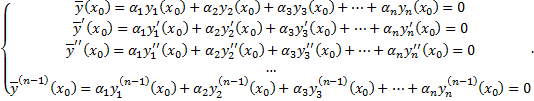
Рассмотрим частное решение ЛОДУ
Оно удовлетворяет в т. начальным условиям
.
Таким образом, частные решения ЛОДУ 
и 
удовлетворяют одним и тем же начальным условиям задачи Коши. По теореме о единственности решения задачи Коши 
, т.е.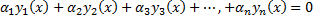 
, т.е. – линейно зависимы на – противоречит условию линейной независимости .
Т.е. 
Замечание. Пусть – частные решения ЛОДУ 
. График функции 
может иметь вид (см. рис. 37, 38):
 Рис. 37 |  Рис. 38 |
| (для линейно независимых решений) | (для линейно зависимых решений) |
Не может иметь вид (см. рис. 39, 40):
 Рис. 39 |  Рис. 40 |
Теорема о размерности пространства решений ЛОДУ n-го порядка. Фундаментальная система решений. Структура общего решения.
