Н.И. КАЛЯДИН
Практикум
По дискретной математике
(часть III. Функции алгебры логики)
Учебно-методическое издание
Николай Иванович Калядин
Практикум
По дискретной математике
(часть III. Функции алгебры логики)
В авторской редакции
Компьютерная верстка Пономарев Е.В.
Подписано в печать Бумага офсетная.
Формат 60 х 84/16. Печать офсетная. Усл. печ. л. .
Уч.-изд. л. . Тираж 50экз. Заказ № .
Отпечатано в типографии издательства ИжГТУ.
Издательство Ижевского государственного технического
университета. 426069, Ижевск, Студенческая, 7
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
“Ижевский государственный технический университет”
Кафедра “Прикладная математика и информатика”
Н.И. КАЛЯДИН
Практикум
По дискретной математике
(часть III. Функции алгебры логики)
 |
Ижевск 2006
19. 20. 21.
 | |
 |
22. 23. 24.
|
Оглавление.
Предисловие………………………………………………………………….......4
Функции алгебры логики……………………………………………....5
Основные определения……………………………………………….5
Элементарные функции алгебры логики……………………………6
Выражение одних элементарных функций через другие ………….8
Свойства конъюнкции, дизъюнкции и отрицания………………….9
Свойства сложения по модулю два, импликации и функции
Шеффера и Вебба ……………………………………….....................9
Аналитические формы представления ФАЛ………………………10
Основные классы функций алгебры логики ……………………….16
Методы определения линейности ФАЛ…………………………….17
Функционально замкнутые классы. Критерий полноты………….19
Задания к практическим занятиям, выполнению расчетно-графических работ и для самостоятельной работы по функциям алгебры
логики……………………………………………………………………...24
Задачи и упражнения Iго типа……………………………………….24
Задачи и упражнения IIго типа………………………………............27
Задачи и упражнения IIIго типа………………………………...........32
Список литературы……………………………………………………………..39
21. (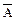
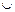 B) + (
B) + (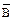
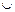 A) = (A
A) = (A  B) + (A
B) + (A 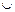 B);
B);
(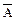
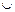 B)
B)  (
(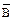
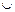 C)
C) 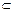 (
(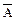
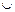 C);
C);
a + (c – b) = (a ~ c) + (b | c);
22. A + B = (A – B) + (B – A);
C  (A
(A 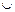 B), если C
B), если C  A, C
A, C  B;
B;
(a 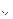 b)
b) 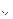 ((
((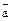 | c)
| c) 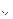 (
(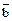 | d) = a
| d) = a 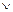 b.
b.
23. (A – B) + ((A + C)  B) = (A – C) + ((A + B)
B) = (A – C) + ((A + B)  C);
C);
C  (A
(A 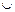 B), если A
B), если A 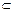 C;
C;
((a | b) 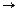 (b
(b 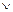 c))
c)) 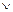 (c ~ d) = d
(c ~ d) = d 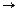 (c
(c 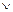 b).
b).
24. (A + (A – B))  (1 – B) = 0;
(1 – B) = 0;
((A – C) 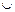 (B – A))
(B – A)) 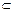 (A
(A 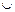 B);
B);
a ~ (b | c) = (a 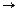 b) ~ (a +c)
b) ~ (a +c) 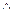 b.
b.
| 1. | 2. | 3. | ||

| 
| 
| ||
| 4. | 5. | 6. | ||

| 
| 
|
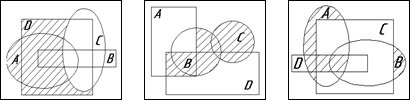
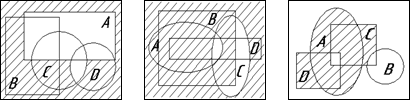
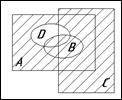
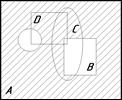
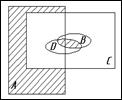
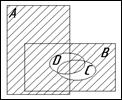
5. Ниже приведены диаграммы Эйлера – Венна. Представьте заштрихованные и отдельно не заштрихованные области максимально компактными аналитическими выражениями, в которых бы использовалось минимальное количество логических операций и букв. С этой целью сначала выразите все заштрихованные области через конституенты – конъюнкты, а незаштрихованные через конституенты – дизъюнкты, и только после этого приступаете к упрощению совершенных форм (результаты проверьте на таблицах истинности).
ГЛАВА 1. Функции алгебры логики
Основные определения
Рассмотрим множество векторов X={< 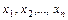 >}, где
>}, где  , x
, x 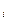
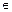 {0, 1},
{0, 1},  =
= 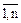 , |
, |  | = 2n. Произведем однозначное отображение множества X на множество Y={0, 1}, т.е.
| = 2n. Произведем однозначное отображение множества X на множество Y={0, 1}, т.е. 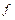 : X
: X 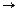 Y.
Y.
Определение 1. Функцией алгебры логики (ФАЛ или логической функцией) называется отображение вида 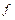 : {0, 1}n
: {0, 1}n 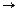 {0, 1}.
{0, 1}.
Так как число различных наборов значений аргументов является конечным, то любая ФАЛ может быть полностью задана таблицей истинности. В левой части этой таблицы перепишем все наборы значений аргументов этой функции, а в правой части – значений функций на этих наборах.
Определение 2. Если две функции алгебры логики 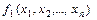 и
и 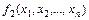 принимают на все возможных наборах значений аргументов одинаковые значения, то функции
принимают на все возможных наборах значений аргументов одинаковые значения, то функции 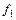 и
и 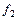 называются равными.
называются равными.
Определение 3. Функция 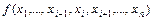 существенно зависит от аргумента
существенно зависит от аргумента 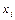 , если имеет место соотношение:
, если имеет место соотношение:

Теорема 1. Число различных функции алгебры логики, зависящих от n аргумента, конечно и равно 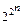 .
.
 2020-07-12
2020-07-12 185
185







